




Next: Locking or Purging a
Up: Implicitly Restarted Lanczos Method
Previous: Deflation and Stopping Rules
Contents
Index
Orthogonal Deflating Transformation
We shall utilize a special orthogonal transformation to implement the
deflation schemes mentioned above. The deflation schemes are related to an eigenvector
associated with a Ritz value that is to be deflated (either locked or purged).
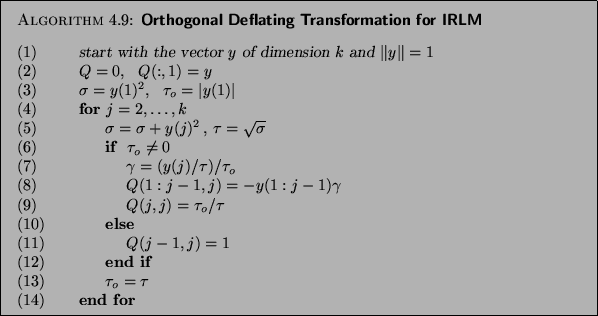
Given a vector 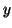 of unit length, the algorithm shown in
Algorithm 4.9 computes an
orthogonal matrix
of unit length, the algorithm shown in
Algorithm 4.9 computes an
orthogonal matrix 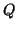 such that
such that 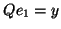 (hence
(hence 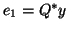 ).
This orthogonal matrix has a very special form and may be written as
Q = R + y e_1^*, with
R e_1 = 0 , R^* y = 0,
where
).
This orthogonal matrix has a very special form and may be written as
Q = R + y e_1^*, with
R e_1 = 0 , R^* y = 0,
where 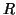 is upper triangular. It may also be written as
Q = L + y g^* , with
L e_1 = 0 , L^* y = e_1 - g,
where
is upper triangular. It may also be written as
Q = L + y g^* , with
L e_1 = 0 , L^* y = e_1 - g,
where 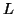 is lower triangular
and
is lower triangular
and
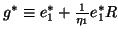 .
Here we assume that
.
Here we assume that
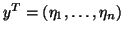 .
.
Now, consider the matrix 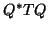 . The
substitutions
. The
substitutions
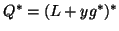 ,
,
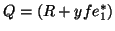 from (4.24) and (4.23)
and the facts
from (4.24) and (4.23)
and the facts
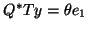 and
and 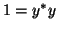 will give
Q^* T Q &=& Q^* T ( R + y e_1^*)
will give
Q^* T Q &=& Q^* T ( R + y e_1^*)
&=& (L^* + g y^*) T R + e_1 e_1^*
&=& L^*TR + g y^*T R + e_1 e_1^*.
Since both 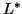 and
and 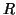 are upper triangular, it follows
that
are upper triangular, it follows
that 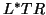 is upper Hessenberg
with the first row and the first column each being zero
due to
is upper Hessenberg
with the first row and the first column each being zero
due to
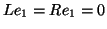 . Also,
. Also,
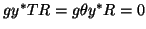 .
From this we conclude that
.
From this we conclude that 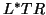 must also be symmetric and hence
tridiagonal. Therefore, we see that
must also be symmetric and hence
tridiagonal. Therefore, we see that
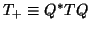 is of the form
is of the form
where 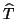 is symmetric and tridiagonal.
is symmetric and tridiagonal.
It should be noted that, as computed by Algorithm 4.9,
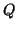 will have componentwise relative
errors on the order of machine precision
will have componentwise relative
errors on the order of machine precision 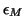 with no
element growth.
with no
element growth.
Subsections





Next: Locking or Purging a
Up: Implicitly Restarted Lanczos Method
Previous: Deflation and Stopping Rules
Contents
Index
Susan Blackford
2000-11-20
![]() . The
substitutions
. The
substitutions
![]() ,
,
![]() from (4.24) and (4.23)
and the facts
from (4.24) and (4.23)
and the facts
![]() and
and ![]() will give
Q^* T Q &=& Q^* T ( R + y e_1^*)
will give
Q^* T Q &=& Q^* T ( R + y e_1^*)
![]() and
and ![]() are upper triangular, it follows
that
are upper triangular, it follows
that ![]() is upper Hessenberg
with the first row and the first column each being zero
due to
is upper Hessenberg
with the first row and the first column each being zero
due to
![]() . Also,
. Also,
![]() .
From this we conclude that
.
From this we conclude that ![]() must also be symmetric and hence
tridiagonal. Therefore, we see that
must also be symmetric and hence
tridiagonal. Therefore, we see that
![]() is of the form
is of the form
![]() will have componentwise relative
errors on the order of machine precision
will have componentwise relative
errors on the order of machine precision ![]() with no
element growth.
with no
element growth.