


Next: Discussion
Up: Literature overview
Previous: Back to Example
Ohta et al. [14] aim at determining the best tile size under the
following hypotheses:
- (H1)
- There are P available processors interconnected as a ring.
- (H2)
- The computation domain is a two-dimensional rectangle of size
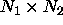 .
.
- (H3)
- Tiles are rectangular and their edges are parallel to the axes
(see Figure 2). The size of a tile is
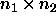 , where
, where 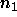 and
and 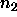 are unknowns.
are unknowns.
- (H4)
- Dependences between tiles are summarized by the vector pair
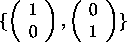 (as in Example 1).
(as in Example 1).
- (H5)
- Tiles are assigned to processor using a one-dimensional cyclic distribution: in other words, tile (i,j) is allocated to
processor
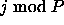 .
.
- (H6)
- The scheduling of the tiles is column-wise:
at step 0, processor
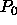 executes tile (0,0) and the computed value is communicated to the adjacent processor
executes tile (0,0) and the computed value is communicated to the adjacent processor 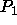 (more precisely, a rectangular
slice of width w and height
(more precisely, a rectangular
slice of width w and height 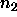 is sent). At step 1,
processors
is sent). At step 1,
processors 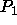 and
and 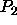 execute tiles (0,1) and (1,0) simultaneously.
After having executed a whole column of tiles, a processor moves on to its
next column.
execute tiles (0,1) and (1,0) simultaneously.
After having executed a whole column of tiles, a processor moves on to its
next column.
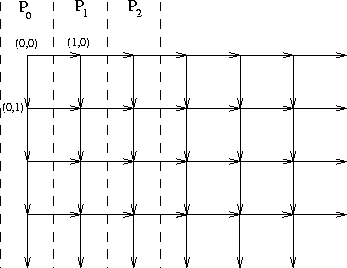
Figure 2: Mapping rectangular tiles onto a ring of processors.
A step is the time required to compute a tile and to communicate data.
Ohta et al. [14] use the following expression:
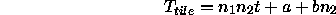
where t is the elemental computation time, a is a communication start-up
and b is the inverse of the communication bandwidth times the width w
of the slice being communicated (the communication cost is a
linear expression in the message size).
To compute the total execution time, Ohta et al. [14] use the
formula 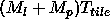 , where
, where 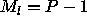 is the latency (the step
at which the last processor begins to work) and
is the latency (the step
at which the last processor begins to work) and 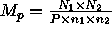 is the number of tiles per processor (assumed to be an integer). Using the approximation
is the number of tiles per processor (assumed to be an integer). Using the approximation 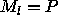 , they derive the total execution time T as
, they derive the total execution time T as
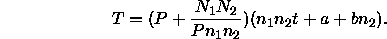
The execution time is found to be minimal when choosing
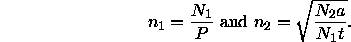



Next: Discussion
Up: Literature overview
Previous: Back to Example
Jack Dongarra
Sat Feb 8 08:17:58 EST 1997
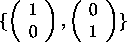 (as in Example 1).
(as in Example 1).
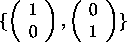 (as in Example 1).
(as in Example 1).

![]()
![]() , where
, where ![]() is the latency (the step
at which the last processor begins to work) and
is the latency (the step
at which the last processor begins to work) and ![]() is the number of tiles per processor (assumed to be an integer). Using the approximation
is the number of tiles per processor (assumed to be an integer). Using the approximation ![]() , they derive the total execution time T as
, they derive the total execution time T as
![]()
![]()