Compressed Diagonal Storage (CDS)





Next: Jagged Diagonal Storage
Up: Survey of Sparse
Previous: Block Compressed Row
If the matrix  is banded with bandwidth that is fairly constant
from row to row,
then it is worthwhile to take advantage of this
structure in the storage scheme by storing subdiagonals of the matrix
in consecutive locations. Not only can we eliminate the vector
identifying the column and row, we can pack the nonzero elements in such a
way as to make the matrix-vector product more efficient.
This storage scheme is particularly useful if the matrix arises from
a finite element or finite difference discretization on a tensor
product grid.
is banded with bandwidth that is fairly constant
from row to row,
then it is worthwhile to take advantage of this
structure in the storage scheme by storing subdiagonals of the matrix
in consecutive locations. Not only can we eliminate the vector
identifying the column and row, we can pack the nonzero elements in such a
way as to make the matrix-vector product more efficient.
This storage scheme is particularly useful if the matrix arises from
a finite element or finite difference discretization on a tensor
product grid.
We say that the matrix 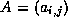 is
banded if there are nonnegative constants
is
banded if there are nonnegative constants 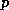 ,
, 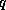 , called the left and
right halfbandwidth, such
that
, called the left and
right halfbandwidth, such
that 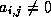 only if
only if 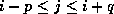 . In this case, we can
allocate for the matrix
. In this case, we can
allocate for the matrix  an array val(1:n,-p:q).
The declaration with reversed dimensions (-p:q,n) corresponds to the
LINPACK band format [73], which unlike CDS,
does not allow for an
efficiently vectorizable matrix-vector multiplication if
an array val(1:n,-p:q).
The declaration with reversed dimensions (-p:q,n) corresponds to the
LINPACK band format [73], which unlike CDS,
does not allow for an
efficiently vectorizable matrix-vector multiplication if 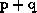 is small.
is small.
Usually, band formats involve storing some zeros. The CDS
format may even contain some array elements that do not
correspond to matrix elements at all.
Consider the nonsymmetric matrix  defined by
defined by
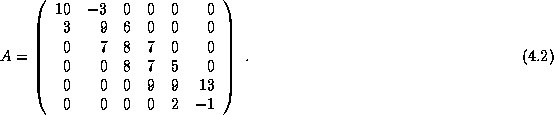
Using the CDS format, we
store this matrix  in an array of dimension (6,-1:1) using
the mapping
in an array of dimension (6,-1:1) using
the mapping

Hence, the rows of the val(:,:) array are

.
Notice the two zeros corresponding to non-existing matrix elements.
A generalization of the CDS format more suitable for manipulating
general sparse matrices on vector supercomputers is discussed by
Melhem in [154]. This variant of CDS uses a stripe data structure to store the matrix  . This structure is
more efficient in storage in the case of varying bandwidth, but it
makes the matrix-vector product slightly more expensive, as it
involves a gather operation.
. This structure is
more efficient in storage in the case of varying bandwidth, but it
makes the matrix-vector product slightly more expensive, as it
involves a gather operation.
As defined in [154],
a stripe in the  matrix
matrix  is a set of positions
is a set of positions
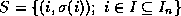 , where
, where 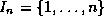 and
and  is a strictly increasing function.
Specifically, if
is a strictly increasing function.
Specifically, if 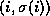 and
and 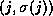 are in
are in 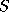 ,
then
,
then

When computing the
matrix-vector product 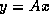 using stripes, each
using stripes, each
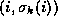 element of
element of  in stripe
in stripe 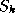 is multiplied
with both
is multiplied
with both 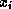 and
and 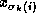 and these products are
accumulated in
and these products are
accumulated in 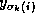 and
and 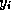 , respectively. For
the nonsymmetric matrix
, respectively. For
the nonsymmetric matrix  defined by
defined by
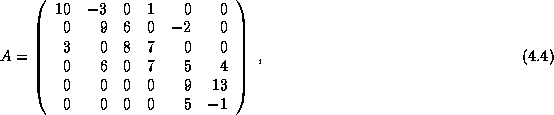
the 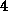 stripes of the matrix
stripes of the matrix  stored
in the rows of the val(:,:) array would be
stored
in the rows of the val(:,:) array would be

.





Next: Jagged Diagonal Storage
Up: Survey of Sparse
Previous: Block Compressed Row
Jack Dongarra
Mon Nov 20 08:52:54 EST 1995
 is banded with bandwidth that is fairly constant
from row to row,
then it is worthwhile to take advantage of this
structure in the storage scheme by storing subdiagonals of the matrix
in consecutive locations. Not only can we eliminate the vector
identifying the column and row, we can pack the nonzero elements in such a
way as to make the matrix-vector product more efficient.
This storage scheme is particularly useful if the matrix arises from
a finite element or finite difference discretization on a tensor
product grid.
is banded with bandwidth that is fairly constant
from row to row,
then it is worthwhile to take advantage of this
structure in the storage scheme by storing subdiagonals of the matrix
in consecutive locations. Not only can we eliminate the vector
identifying the column and row, we can pack the nonzero elements in such a
way as to make the matrix-vector product more efficient.
This storage scheme is particularly useful if the matrix arises from
a finite element or finite difference discretization on a tensor
product grid.
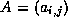 is
banded if there are nonnegative constants
is
banded if there are nonnegative constants 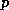 ,
, 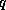 , called the left and
right halfbandwidth, such
that
, called the left and
right halfbandwidth, such
that 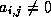 only if
only if 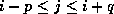 . In this case, we can
allocate for the matrix
. In this case, we can
allocate for the matrix 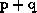 is small.
is small.
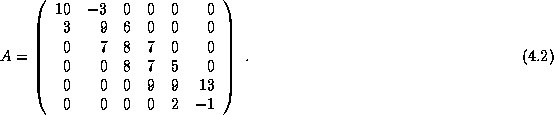


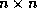 matrix
matrix 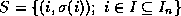 , where
, where 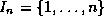 and
and  is a strictly increasing function.
Specifically, if
is a strictly increasing function.
Specifically, if 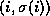 and
and 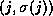 are in
are in 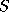 ,
then
,
then
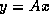 using stripes, each
using stripes, each
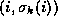 element of
element of 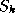 is multiplied
with both
is multiplied
with both 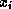 and
and 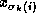 and these products are
accumulated in
and these products are
accumulated in 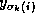 and
and 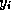 , respectively. For
the nonsymmetric matrix
, respectively. For
the nonsymmetric matrix 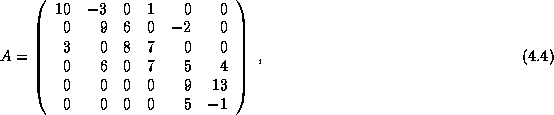
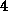 stripes of the matrix
stripes of the matrix 