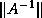
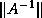
Bounds on the error 
inevitably rely on bounds for 
,
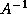since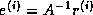 
. There is a large number of problem dependent
ways to estimate 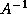; we mention a few here.
When a splitting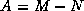 
is used to get an iteration
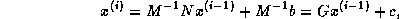
then the matrix whose
inverse norm we need is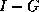 
. Often, we know how to estimate
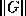if the splitting is a standard one such as Jacobi or SOR,
and the matrix 
has special characteristics such as Property A.
Then we may estimate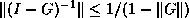 
.
When is symmetric positive definite, and Chebyshev acceleration with
adaptation of parameters is being used, then at each step the algorithm
estimates the largest and smallest eigenvalues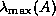 
and
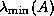of anyway.
Since is symmetric positive definite,
.
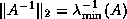This adaptive estimation is often done using the Lanczos algorithm
(see section 
),
which can usually provide good estimates of the
largest (rightmost) and smallest (leftmost) eigenvalues of a symmetric matrix
at the cost of a few matrix-vector multiplies.
For general nonsymmetric , we may apply
the Lanczos method to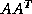 
or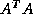 
,
and use the fact that
.
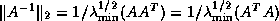It is also possible to estimate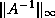 
provided one is willing
to solve a few systems of linear equations with and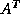 
as coefficient
matrices. This is often done with dense linear system solvers, because the
extra cost of these systems is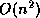 
, which is small compared to the cost
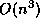of the LU decomposition (see Hager [121],
Higham [124] and Anderson, et al. [3]).
This is not the case for iterative solvers, where the cost of these
solves may well be several times as much as the original linear system.
Still, if many linear systems with the same coefficient matrix and
differing right-hand-sides are to be solved, it is a viable method.
The approach in the last paragraph also lets us estimate the alternate
error bound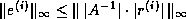 
.
This may be much smaller than the simpler
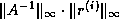in the
case where the rows of are badly scaled; consider the case of a
diagonal matrix with widely varying diagonal entries. To
compute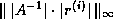 
, let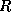 
denote the diagonal
matrix with diagonal entries equal to the entries of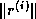 
; then
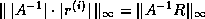(see Arioli, Demmel and Duff [5]). 
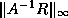can be estimated using the
technique in the last paragraph since multiplying by
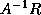or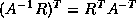 
is no harder than multiplying
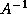by and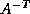 
and also by 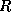, a diagonal matrix.