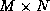 matrix
matrix 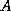 , we seek the factorization
, we seek the factorization 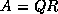 ,
where
,
where 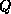 is an
is an 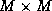 orthogonal matrix, and
orthogonal matrix, and 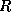 is an
is an 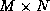 upper triangular matrix.
At the
upper triangular matrix.
At the  -th step of the computation, we partition this factorization
to the
-th step of the computation, we partition this factorization
to the 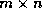 submatrix of
submatrix of 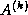 as
as
Given an 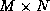 matrix
matrix 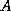 , we seek the factorization
, we seek the factorization 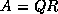 ,
where
,
where 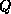 is an
is an 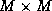 orthogonal matrix, and
orthogonal matrix, and 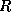 is an
is an 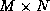 upper triangular matrix.
At the
upper triangular matrix.
At the  -th step of the computation, we partition this factorization
to the
-th step of the computation, we partition this factorization
to the 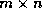 submatrix of
submatrix of 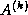 as
as
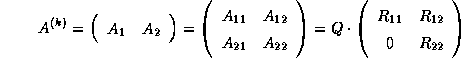
where the block 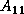 is
is 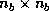 ,
,
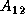 is
is 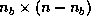 ,
,
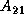 is
is 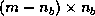 , and
, and 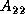 is
is 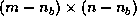 .
.
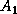 is an
is an 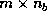 matrix, containing the first
matrix, containing the first 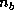 columns of
the matrix
columns of
the matrix 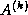 , and
, and 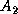 is an
is an  matrix,
containing the last
matrix,
containing the last 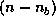 columns of
columns of 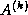 (that is,
(that is, 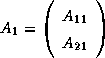 and
and 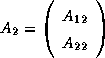 ).
).
 is a
is a 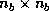 upper triangular matrix.
upper triangular matrix.
A QR factorization is performed on the first 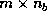 panel of
panel of 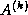 (i.e.,
(i.e., 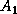 ).
In practice,
).
In practice, 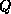 is computed by applying a series of Householder
transformations to
is computed by applying a series of Householder
transformations to 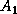 of the form,
of the form, 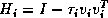 where
where 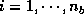 . The vector
. The vector 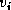 is of length
is of length 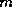 with
0's for the first
with
0's for the first  entries and 1 for the
entries and 1 for the 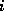 -th entry, and
-th entry, and
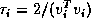 . During the QR factorization, the vector
. During the QR factorization, the vector 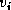 overwrites the entries of
overwrites the entries of 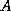 below the diagonal, and
below the diagonal, and 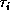 is stored
in a vector.
Furthermore, it can be shown that
is stored
in a vector.
Furthermore, it can be shown that 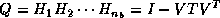 ,
where
,
where 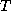 is
is 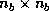 upper triangular and the
upper triangular and the 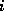 -th column of
-th column of 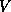 equals
equals 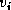 .
This is indeed a block version of the QR factorization [22][4],
and is rich in matrix-matrix operations.
.
This is indeed a block version of the QR factorization [22][4],
and is rich in matrix-matrix operations.
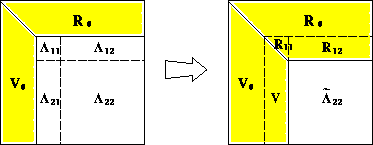
Figure 4: A snapshot of block QR factorization.
The block equation can be rearranged as
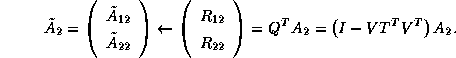
A snapshot of the block QR factorization is shown in Figure 4.
During the computation, the sequence of the Householder vectors 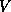 is
computed, and the row panel
is
computed, and the row panel  and
and 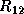 , and the trailing
submatrix
, and the trailing
submatrix 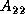 are updated.
The factorization can be done by recursively applying the steps
outlined above to the
are updated.
The factorization can be done by recursively applying the steps
outlined above to the 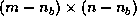 matrix
matrix 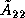 .
.
The computation of the above steps of the LAPACK routine, DGEQRF, involves the following operations:
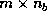 panel of
panel of
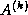 (i.e.,
(i.e., 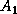 )
)
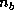 times (
times (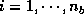 ) ]
) ]
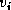 and
and 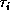
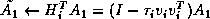
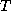 of the block reflector
of the block reflector 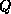
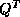 to the rest of the matrix from the left
to the rest of the matrix from the left
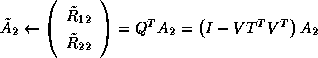
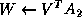
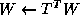

The corresponding steps of the ScaLAPACK routine, PDGEQRF, are as follows:
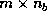 panel of
panel of 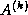 (i.e.,
(i.e., 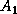 )
)
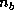 times (
times (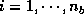 ) ]
) ]
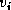 and
and 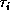
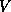 , computes
, computes 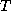 only in the current process
row.
only in the current process
row.
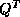 to the rest of the matrix from the left
to the rest of the matrix from the left
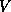 is broadcast rowwise across all columns of
processes. The transpose of
is broadcast rowwise across all columns of
processes. The transpose of 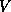 is locally multiplied by
is locally multiplied by 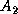 ,
then the products are added to the current process row
(
,
then the products are added to the current process row
(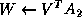 ).
).
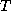 is broadcast rowwise in the current process
row to all columns of processes and multiplied with the sum
(
is broadcast rowwise in the current process
row to all columns of processes and multiplied with the sum
(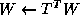 ).
).
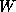 is broadcast columnwise down all rows of
processes. Now, processes have their own portions of
is broadcast columnwise down all rows of
processes. Now, processes have their own portions of 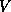 and
and 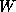 , then they update
the local portions of the matrix
, then they update
the local portions of the matrix 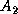 (
( ).
).