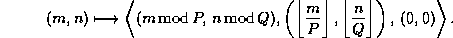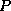 ,
, 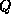 ,
, 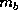 , and
, and 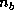 , where
, where 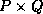 is the
process grid and
is the
process grid and 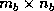 is the block size.
Blocks separated by a fixed stride in the column and row
directions are assigned to the same process.
is the block size.
Blocks separated by a fixed stride in the column and row
directions are assigned to the same process.
The way in which a matrix is distributed over the processes
has a major impact on the load balance and
communication characteristics of the concurrent algorithm, and hence
largely determines its performance and scalability.
The block cyclic distribution provides a simple, yet
general-purpose way of distributing a block-partitioned matrix on
distributed memory concurrent computers.
The block cyclic data distribution is parameterized by the four
numbers 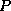 ,
, 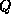 ,
, 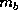 , and
, and 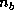 , where
, where 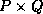 is the
process grid and
is the
process grid and 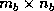 is the block size.
Blocks separated by a fixed stride in the column and row
directions are assigned to the same process.
is the block size.
Blocks separated by a fixed stride in the column and row
directions are assigned to the same process.
Suppose we have 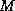 objects indexed by the integers
objects indexed by the integers 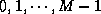 .
In the block cyclic data distribution the mapping of the global index,
.
In the block cyclic data distribution the mapping of the global index, 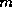 ,
can be expressed as
,
can be expressed as 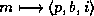 ,
where
,
where 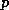 is the logical
process number,
is the logical
process number, 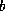 is the block number in process
is the block number in process 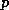 , and
, and
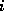 is the index within block
is the index within block 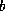 to which
to which 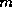 is mapped.
Thus, if the number of data objects in a block is
is mapped.
Thus, if the number of data objects in a block is 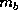 ,
the block cyclic data distribution may be written as follows:
,
the block cyclic data distribution may be written as follows:
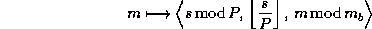
where 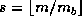 and
and 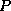 is the number of processes.
The distribution of a block-partitioned matrix can be regarded as the
tensor product of two such mappings: one that distributes
the rows of the matrix over
is the number of processes.
The distribution of a block-partitioned matrix can be regarded as the
tensor product of two such mappings: one that distributes
the rows of the matrix over 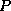 processes, and another that distributes
the columns over
processes, and another that distributes
the columns over 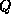 processes. That is, the matrix element
indexed globally by
processes. That is, the matrix element
indexed globally by 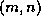 can be written as
can be written as
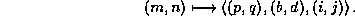
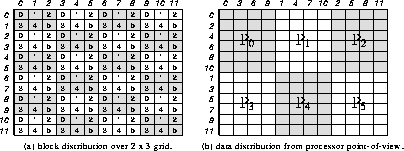
Figure 1: Example of a block cyclic data distribution.
Figure 1 (a) shows an example of the block cyclic data
distribution, where a matrix with 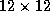 blocks
is distributed over a
blocks
is distributed over a 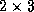 grid.
The numbered squares represent blocks of elements, and the number indicates
at which location in the process grid the block is stored - all blocks
labeled with the same number are stored in the same process.
The slanted numbers, on the left and on the top of the matrix,
represent indices of a row of blocks and of a column of blocks, respectively.
Figure 1 (b) reflects the distribution from a process
point-of-view. Each process has
grid.
The numbered squares represent blocks of elements, and the number indicates
at which location in the process grid the block is stored - all blocks
labeled with the same number are stored in the same process.
The slanted numbers, on the left and on the top of the matrix,
represent indices of a row of blocks and of a column of blocks, respectively.
Figure 1 (b) reflects the distribution from a process
point-of-view. Each process has 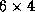 blocks.
The block cyclic data distribution is the only distribution supported by
the ScaLAPACK routines. The block cyclic data distribution can reproduce
most data distributions used in linear algebra computations.
For example, one-dimensional distributions over rows or columns
are obtained by choosing
blocks.
The block cyclic data distribution is the only distribution supported by
the ScaLAPACK routines. The block cyclic data distribution can reproduce
most data distributions used in linear algebra computations.
For example, one-dimensional distributions over rows or columns
are obtained by choosing 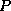 or
or 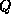 to be 1.
to be 1.
The non-scattered decomposition (or pure block distribution) is just a
special case of the cyclic distribution in which the block size is given by
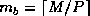 and
and 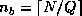 .
That is,
.
That is,
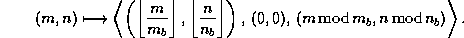
Similarly a purely scattered decomposition (or two dimensional wrapped
distribution) is another special case in which the block size is given
by 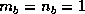 ,
,