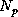The performance results in Figures 6,
8, and 10
can be used to assess the scalability of the
factorization routines. In general, concurrent efficiency, 
,
is defined as the concurrent speedup per process. That is,
for the given problem size, 
, on the number of processes used,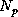 
,
where 
is the time for a problem of size to run
on 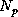processes,
and 
is the time to run on one process using the best sequential
algorithm.
Another approach to investigate the efficiency is to see
how the performance per process degrades as the number of processes
increases for a fixed grain size, i. e., by plotting
isogranularity curves in the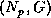 
plane, where 
is the performance.
Since
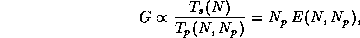
the scalability for memory-constrained problems can readily be accessed by the extent to which the isogranularity curves differ from linearity. Isogranularity was first defined in [24], and later explored in [20][21].
Figure 11 shows the isogranularity plots for the ScaLAPACK factorization routines on the Paragon. The matrix size per process is fixed at 5 and 20 Mbytes on the Paragon. Refer to Figures 6, 8, and 10 for block size and process grid size characteristics. The near-linearity of these plots shows that the ScaLAPACK routines are quite scalable on this system.
Figure 11: Scalability of factorization routines on the Intel Paragon (5, 20 Mbytes/node).