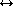 hit association:
hit association:





Given the preceding prescription for estimating the state of a single target
from a sequence of two-dimensional observations, the central issue in multitarget
tracking is that of associating observations with tracks or observations on
one scan with those of a subsequent scan (e.g., in Figure 18.16,
which x is paired with which o). There are, in a sense, two extreme
schemes for attempting this track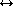 hit association:
hit association:
The track splitting model is robust in the sense that the correct
track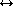 hit association is very likely to be generated and
maintained at any step in track processing. The track extension task is also
extremely ``localized,'' in the sense that splittings of any one track can be
done independently of those for other tracks. This makes concurrent
implementations of track splitting quite simple.
The primary objections to track splitting are twofold:
hit association is very likely to be generated and
maintained at any step in track processing. The track extension task is also
extremely ``localized,'' in the sense that splittings of any one track can be
done independently of those for other tracks. This makes concurrent
implementations of track splitting quite simple.
The primary objections to track splitting are twofold:
The optimal association prescription is orthogonal to track splitting in the
sense that the single ``best'' pairing is maintained in place of all plausible
pairings. This best Track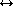 Hit association is determined by a
global optimization procedure, as follows. Let
Hit association is determined by a
global optimization procedure, as follows. Let 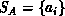 and
and
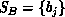 be two lists of items (e.g., actual data and predicted data
values). Let
be two lists of items (e.g., actual data and predicted data
values). Let
be a cost for associating items 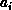 and
and 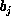 (e.g., the cartesian distance
between predicted and actual data positions for the data coordinates defined
above). The optimal association of the two lists is that particular
permutation,
(e.g., the cartesian distance
between predicted and actual data positions for the data coordinates defined
above). The optimal association of the two lists is that particular
permutation,
such that the total association score,
is minimized over all permutations 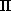 of Equation 18.4.
of Equation 18.4.
Leaving aside, for now, the question of computational costs associated with the minimization of Equation 18.5, there are some fundamental difficulties associated with the use of optimal associators in multitarget tracking models. In particular
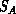 and
and 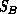 do
not correspond to the same sets of underlying targets.
do
not correspond to the same sets of underlying targets.
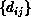 can lead to global
distortions of the globally optimal association.
can lead to global
distortions of the globally optimal association.




