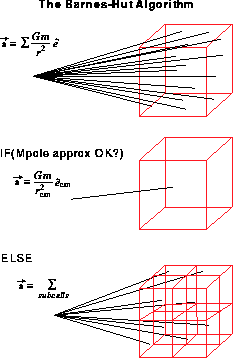
Figure 12.12: The Barnes-Hut Algorithm





Once the distribution of matter is represented on a number of length scales, it is possible to use the approximation in Equation 12.5 to reduce the number of operations required to find the force on a body. The force on each body is computed independently by a recursive procedure that traverses the tree from the top down. Beginning at the root of the tree, we simply apply a multipole acceptability criterion (MAC). This tells us whether Equation 12.5 (or an appropriate higher-order approximation) is sufficiently accurate. If it is, then we evaluate the approximation, and eliminate the summation over all the bodies contained within the node. Otherwise, we proceed recursively to the eight daughter cells of the node. Whenever we reach a terminal node, we simply compute the body-body interaction. The procedure is shown schematically in Figure 12.12.

Figure 12.12: The Barnes-Hut Algorithm
The performance of the algorithm depends on how we evaluate the MAC. For
example, one could always answer ``no,'' in which case the performance would
be identical to the 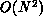 case (although the bookkeeping overhead would be
somewhat higher, and we would not take advantage of Newton's second law).
The specifics of how best to evaluate the MAC would take us far afield
[Barnes:89d], [Makino:90a], and [Salmon:92a].
case (although the bookkeeping overhead would be
somewhat higher, and we would not take advantage of Newton's second law).
The specifics of how best to evaluate the MAC would take us far afield
[Barnes:89d], [Makino:90a], and [Salmon:92a].
Suffice it to say that all methods are based on the idea that the multipole
approximation is accurate when the distance to the cell is large compared to
the size of the cell. Essentially any criterion based on a ratio of
size-of-cell to distance-to-cell will require 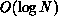 -force evaluations
to compute the total force on each body [Barnes:86a], [Salmon:90a].
Since the forces on all bodies are evaluated independently, the total number
of evaluations is proportional to
-force evaluations
to compute the total force on each body [Barnes:86a], [Salmon:90a].
Since the forces on all bodies are evaluated independently, the total number
of evaluations is proportional to 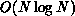 , which is a substantial
improvement over the
, which is a substantial
improvement over the 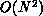 situation that results from a naive evaluation
of Equation 12.3.
situation that results from a naive evaluation
of Equation 12.3.




