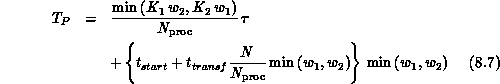Next: 8.1.4 Systems of Linear
Up: 8.1 Full and Banded
Previous: 8.1.2 Basic Matrix Arithmetic
Banded Matrix-Vector Multiplication
First, we consider the parallelization of the operation 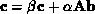 on a linear array of
on a linear array of 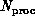 processors when
processors when 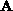 is a banded
is a banded 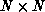 matrix with
matrix with 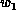 ,
,
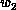 upper and lower bandwidths, and we assume that matrices are
stored using a sparse scheme [Rice:85a]. For simplicity, we
describe the case
upper and lower bandwidths, and we assume that matrices are
stored using a sparse scheme [Rice:85a]. For simplicity, we
describe the case 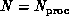 . The proposed implementation is
based on a decomposition of matrix
. The proposed implementation is
based on a decomposition of matrix 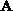 into an upper
into an upper 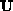 (including the diagonal of
(including the diagonal of 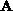 ) and lower
) and lower 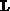 triangular
matrices, such as
triangular
matrices, such as 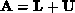 . Furthermore, we
assume that row
. Furthermore, we
assume that row 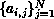 and
and 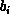 are stored
in processor i. Without loss of generality, we can assume
are stored
in processor i. Without loss of generality, we can assume 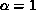 and
and 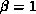 . The vector
. The vector  can then be expressed as
can then be expressed as 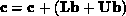 . The products
. The products 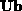 and
and 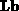 are computed within
are computed within 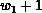 and
and 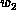 iterations, respectively.
The computation involved is described in Figure 8.3. In
order to compute the complexity of the above algorithm, we assume
without any loss of generality, that
iterations, respectively.
The computation involved is described in Figure 8.3. In
order to compute the complexity of the above algorithm, we assume
without any loss of generality, that 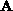 has K non-zero elements,
and
has K non-zero elements,
and 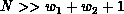 . Then it can be shown that the time complexity is
. Then it can be shown that the time complexity is
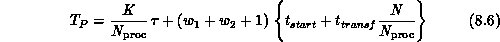
and the memory space required for each subdomain is 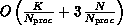 .
.

Figure 8.3: The Pseudo Code for Banded Matrix-Vector Multiplication
Banded Matrix-Matrix Multiplication
Second, we consider the implementation of 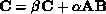 , on a ring of
, on a ring of 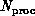 processors when
processors when
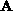 ,
, 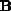 are banded
are banded 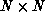 matrices with
matrices with 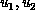 upper,
and
upper,
and 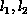 lower bandwidths, respectively. Again, we describe the
realization for
lower bandwidths, respectively. Again, we describe the
realization for 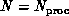 . The case
. The case 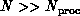 is
straightforward generalization. The processor i computes column
is
straightforward generalization. The processor i computes column
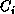 of matrix
of matrix  and holds one row of matrix
and holds one row of matrix 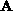 (denoted by
(denoted by
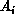 ) and a column of matrix
) and a column of matrix 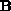 (denoted by
(denoted by 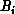 ).
).
The algorithm consists of two phases as in banded-matrix vector
multiplication. Without loss of generality, we can assume 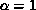 , and
, and 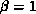 . In the first phase, each node starts by
calculating
. In the first phase, each node starts by
calculating 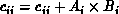 , then each node i
passes
, then each node i
passes 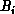 to node i-1, this phase is repeated
to node i-1, this phase is repeated 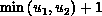 times. In the second phase, each node restores
times. In the second phase, each node restores
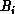 and passes it to node i+1. This phase is repeated
and passes it to node i+1. This phase is repeated 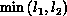 times. The implementation proposed for this operation is
described in Figure 8.4.
times. The implementation proposed for this operation is
described in Figure 8.4.

Figure 8.4: The Pseudo Code for Banded Matrix-Matrix Multiplication
Without loss of generality, we assume that 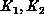 are the number
of non-zero elements for the matrices
are the number
of non-zero elements for the matrices 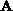 ,
, 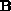 respectively,
and denote by
respectively,
and denote by 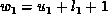 and
and 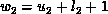 . Then
we can show that the parallel execution time
. Then
we can show that the parallel execution time 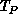 is given by
is given by
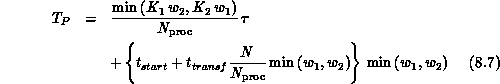
The above realization has been implemented on the nCUBE-1
[Chrisochoides:90a]. Tables 8.1 and 8.2 indicate
the performance of BLAS 2 computation
for a block tridiagonal matrix where each block is dense. In these
experiments, each processor has the same computation to perform. The
results indicate very satisfactory performance for these type of data.
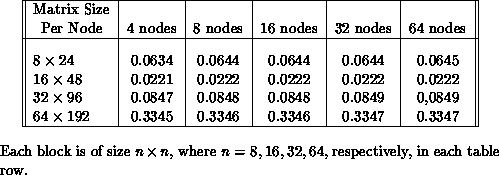
Table 8.1: Measured maximum total elapsed time (in seconds) for
multiplication of a block tridiagonal matrices with a vector.

Table 8.2: Measured maximum elapsed time (in seconds) for multiplication
of a block tridiagonal matrix by a block tridiagonal matrix.





Next: 8.1.4 Systems of Linear
Up: 8.1 Full and Banded
Previous: 8.1.2 Basic Matrix Arithmetic
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
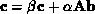 on a linear array of
on a linear array of 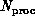 processors when
processors when 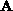 is a banded
is a banded 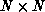 matrix with
matrix with 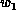 ,
,
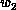 upper and lower bandwidths, and we assume that matrices are
stored using a sparse scheme [Rice:85a]. For simplicity, we
describe the case
upper and lower bandwidths, and we assume that matrices are
stored using a sparse scheme [Rice:85a]. For simplicity, we
describe the case 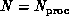 . The proposed implementation is
based on a decomposition of matrix
. The proposed implementation is
based on a decomposition of matrix 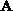 into an upper
into an upper 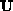 (including the diagonal of
(including the diagonal of 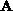 ) and lower
) and lower 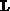 triangular
matrices, such as
triangular
matrices, such as 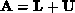 . Furthermore, we
assume that row
. Furthermore, we
assume that row 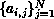 and
and 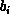 are stored
in processor i. Without loss of generality, we can assume
are stored
in processor i. Without loss of generality, we can assume 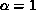 and
and 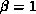 . The vector
. The vector  can then be expressed as
can then be expressed as 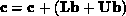 . The products
. The products 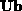 and
and 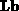 are computed within
are computed within 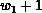 and
and 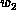 iterations, respectively.
The computation involved is described in Figure 8.3. In
order to compute the complexity of the above algorithm, we assume
without any loss of generality, that
iterations, respectively.
The computation involved is described in Figure 8.3. In
order to compute the complexity of the above algorithm, we assume
without any loss of generality, that 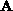 has K non-zero elements,
and
has K non-zero elements,
and 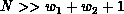 . Then it can be shown that the time complexity is
. Then it can be shown that the time complexity is





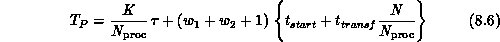
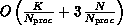 .
.

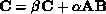 , on a ring of
, on a ring of 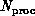 processors when
processors when
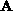 ,
, 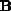 are banded
are banded 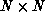 matrices with
matrices with 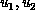 upper,
and
upper,
and 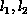 lower bandwidths, respectively. Again, we describe the
realization for
lower bandwidths, respectively. Again, we describe the
realization for 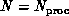 . The case
. The case 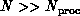 is
straightforward generalization. The processor i computes column
is
straightforward generalization. The processor i computes column
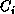 of matrix
of matrix  and holds one row of matrix
and holds one row of matrix 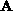 (denoted by
(denoted by
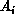 ) and a column of matrix
) and a column of matrix 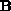 (denoted by
(denoted by 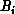 ).
).
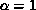 , and
, and 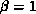 . In the first phase, each node starts by
calculating
. In the first phase, each node starts by
calculating 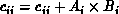 , then each node i
passes
, then each node i
passes 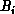 to node i-1, this phase is repeated
to node i-1, this phase is repeated 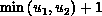 times. In the second phase, each node restores
times. In the second phase, each node restores
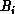 and passes it to node i+1. This phase is repeated
and passes it to node i+1. This phase is repeated 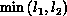 times. The implementation proposed for this operation is
described in Figure
times. The implementation proposed for this operation is
described in Figure 
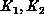 are the number
of non-zero elements for the matrices
are the number
of non-zero elements for the matrices 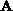 ,
, 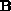 respectively,
and denote by
respectively,
and denote by 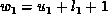 and
and 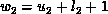 . Then
we can show that the parallel execution time
. Then
we can show that the parallel execution time 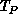 is given by
is given by