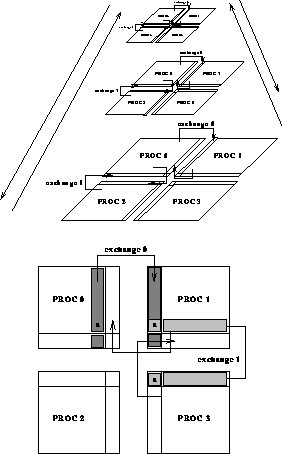
Figure 6.25: Domain Decomposition for Multigrid Computation. Processor communication is on a two-dimensional grid; each processor operates at all levels of the pyramid.





The multigrid algorithm described in the previous section can be executed in many different ways on a parallel computer. One essential distinction that has to be made is related to the number of processors available and the ``size'' of a single processor.
The drawback of implementations on fine grain-size SIMD computers (where we assign one processor to each grid point) is that when iteration is on a coarse scale, all the nodes in the other scales (i.e., the majority of nodes) are idle, and the efficiency of computation is seriously compromised.
Furthermore, if the implementation is on a hypercube parallel computer and the mapping is such that all the communications paths in the pyramid are mapped into communication paths in the hypercube with length bounded by two [Chan:86b], a fraction of the nodes is never used because the total number of grid points is not equal to a power of two. This fraction is one third for two-dimensional problems encountered in vision.
Fortunately, if we use a MIMD computer with powerful processors, sufficient distributed memory, and two-dimensional internode connections (the hypercube contains a two-dimensional mesh), the above problems do not exist.
In this case, a two-dimensional domain decomposition can be used efficiently: A slice of the image with its associated pyramidal structure is assigned to each processor. All nodes are working all the time, switching between different levels of the pyramid as illustrated in Figure 6.25.

Figure 6.25: Domain Decomposition for Multigrid Computation. Processor
communication is on a two-dimensional grid; each processor operates at all
levels of the pyramid.
No modification of the sequential algorithm is needed for points in the image belonging to the interior of the assigned domain. Conversely, points on the boundary need to know values of points assigned to a nearby processor. With this purpose, the assigned domain is extended to contain points assigned to nearby processors, and a communication step before each iteration on a given layer is responsible for updating this strip so that it contains the correct (most recent) values. Two exchanges are sufficient.
The recursive multiscale call mg(lay) is based on an alternation of relaxation steps and discontinuity detection steps as follows (software is written in C language):
{
int i;
if(lay==coarsest)step(lay);
else{ i=na;while(i-)step(lay);
i=nb;if(i!=0)
{up(lay);while(i-)mg(lay-1);down(lay-1);}
i=nc;while(i-)step(lay);
}
}
int step(lay) int lay;
{
exchange_border_strip(lay);
update_line_processes(lay); relax_depth_processes(lay);
}
int mg(lay) int lay;
Each step is preceded by an exchange of data on the border of the assigned domains.
Because the communication overhead is proportional to the linear dimension of the assigned image portion, the efficiency is high as soon as the number of pixels in this portion is large. Detailed results are in [Battiti:91a].




