Overlapping communication and computation





Next: Fewer synchronization points
Up: Inner products
Previous: Inner products
Clearly, in the usual formulation of conjugate gradient-type methods
the inner products induce a synchronization of the
processors, since they cannot progress until the final result has been
computed:
updating 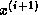 and
and 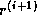 can only begin after
completing the inner product for
can only begin after
completing the inner product for 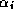 . Since on a
distributed-memory machine communication is needed for the inner product, we
cannot overlap this communication with useful computation.
The same observation applies to updating
. Since on a
distributed-memory machine communication is needed for the inner product, we
cannot overlap this communication with useful computation.
The same observation applies to updating 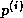 , which can only begin
after completing the inner product for
, which can only begin
after completing the inner product for 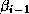 .
.
Figure  shows a variant of CG, in which all
communication time may be overlapped with useful computations. This
is just a reorganized version of the original CG scheme, and is
therefore precisely as stable. Another advantage over other
approaches (see below) is that no additional operations are required.
shows a variant of CG, in which all
communication time may be overlapped with useful computations. This
is just a reorganized version of the original CG scheme, and is
therefore precisely as stable. Another advantage over other
approaches (see below) is that no additional operations are required.
This rearrangement is based on two tricks. The first is that updating
the iterate is delayed to mask the communication stage of the
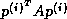 inner product. The second trick relies on splitting the
(symmetric) preconditioner as
inner product. The second trick relies on splitting the
(symmetric) preconditioner as 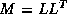 , so one first computes
, so one first computes
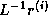 , after which the inner product
, after which the inner product
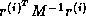 can be computed as
can be computed as  where
where 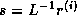 . The
computation of
. The
computation of 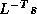 will then mask the communication stage of the
inner product.
will then mask the communication stage of the
inner product.

Figure: A rearrangement of Conjugate Gradient for parallelism
Under the assumptions that we have made, CG can be efficiently parallelized
as follows:
- The communication required for the reduction of the inner
product for
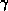 can be overlapped with the update for
can be overlapped with the update for 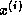 ,
(which could in fact have been done in the previous iteration step).
,
(which could in fact have been done in the previous iteration step).
- The reduction of the inner product for
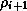 can be
overlapped with the remaining part of the preconditioning operation
at the beginning of the next iteration.
can be
overlapped with the remaining part of the preconditioning operation
at the beginning of the next iteration.
- The computation of a segment of
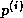 can be followed
immediately by the computation of a segment of
can be followed
immediately by the computation of a segment of 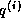 , and this can
be followed by the computation of a part of the inner product. This
saves on load operations for segments of
, and this can
be followed by the computation of a part of the inner product. This
saves on load operations for segments of 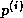 and
and 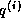 .
.
For a more detailed discussion see Demmel, Heath and
Van der Vorst [67]. This algorithm
can be extended trivially to preconditioners of 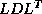 form, and
nonsymmetric preconditioners in the Biconjugate Gradient Method.
form, and
nonsymmetric preconditioners in the Biconjugate Gradient Method.





Next: Fewer synchronization points
Up: Inner products
Previous: Inner products
Jack Dongarra
Mon Nov 20 08:52:54 EST 1995
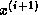 and
and 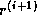 can only begin after
completing the inner product for
can only begin after
completing the inner product for 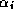 . Since on a
distributed-memory machine communication is needed for the inner product, we
cannot overlap this communication with useful computation.
The same observation applies to updating
. Since on a
distributed-memory machine communication is needed for the inner product, we
cannot overlap this communication with useful computation.
The same observation applies to updating 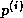 , which can only begin
after completing the inner product for
, which can only begin
after completing the inner product for 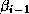 .
.
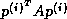 inner product. The second trick relies on splitting the
(symmetric) preconditioner as
inner product. The second trick relies on splitting the
(symmetric) preconditioner as 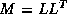 , so one first computes
, so one first computes
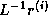 , after which the inner product
, after which the inner product
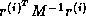 can be computed as
can be computed as  where
where 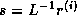 . The
computation of
. The
computation of 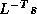 will then mask the communication stage of the
inner product.
will then mask the communication stage of the
inner product.

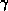 can be overlapped with the update for
can be overlapped with the update for 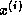 ,
(which could in fact have been done in the previous iteration step).
,
(which could in fact have been done in the previous iteration step).
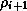 can be
overlapped with the remaining part of the preconditioning operation
at the beginning of the next iteration.
can be
overlapped with the remaining part of the preconditioning operation
at the beginning of the next iteration.
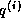 , and this can
be followed by the computation of a part of the inner product. This
saves on load operations for segments of
, and this can
be followed by the computation of a part of the inner product. This
saves on load operations for segments of 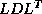 form, and
nonsymmetric preconditioners in the Biconjugate Gradient Method.
form, and
nonsymmetric preconditioners in the Biconjugate Gradient Method.