Implicitly Restarted Arnoldi Method
  R. Lehoucq and D. Sorensen

Perhaps the most successful numerical algorithm for computing the complete eigensystem of a general square matrix $A$ is the implicitly shifted QR algorithm. One of the keys to the success of this method is its relationship to the Schur decomposition

$$A = U T U^{\ast} .$$ (127)

This well-known decomposition asserts that every square matrix $A$ is unitarily similar to an upper triangular matrix $T$.

The QR algorithm produces a sequence of unitary similarity transformations that iteratively reduce $A$ to upper triangular form (see §7.3). In other words, it computes a Schur decomposition. A practical implementation of the QR algorithm begins with an initial unitary similarity transformation of $A$ to the condensed form $V^{\ast} AV = H$ where $H$ is upper Hessenberg (``almost upper triangular'') and $V$ is unitary. Then the following iteration is performed.

		 SHIFTED QR METHOD 


factor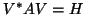 $V^{\ast} AV = H$ 


for $j=1,2,3\ldots,$ until convergence  


select a shift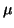 $\mu$ 


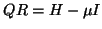
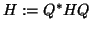
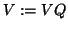
QR-factorize $QR = H - \mu I$ 

$H := Q^{\ast} H Q$ 

$V := VQ$ 


end for  

In this scheme, $Q$ is unitary and $R$ is upper triangular (i.e., the QR factorization of $H-\mu I$). It is easy to see that $H$ is unitarily similar to $A$ throughout the course of this iteration. The iteration is continued until the subdiagonal elements of $H$ converge to zero, i.e., until a Schur decomposition has been (approximately) obtained.

If $U_k$ represents the leading $k$ columns of $U$, and $T_k$ the leading principal $k \times k$ submatrix of $T$ in (7.11), then

$$A U_k = U_k T_k,$$

and we refer to this as a partial Schur decomposition of $A$. Since there is a Schur decomposition with the eigenvalues of $A$ appearing on the diagonal in any given ordering, there is always a partial Schur decomposition of $A$ with the diagonal elements of $T_k$ consisting of any specified subset of $k$ eigenvalues of $A$. Moreover, $\mbox{span}(U_k)$ is an invariant subspace of $A$ for these eigenvalues.

We are going to exploit this aspect of the Schur decomposition. We shall also exploit the fact that a variant of the QR iteration can be devised that will force eigenvalues of interest to appear in this leading $k \times k$ block of $T$ as the iteration proceeds. Our goal will be to develop a truncated form of the QR method that is suitable for computing a selected set of $k$ eigenvalues of a large matrix $A$. We call implicitly restarted Arnoldi method the IRAM.