




Next: Algorithm
Up: Band Lanczos Method
Previous: The Need for Deflation
Contents
Index
Basic Properties
After the first  iterations, the band Lanczos algorithm has
generated the first
iterations, the band Lanczos algorithm has
generated the first  Lanczos vectors (4.28).
These vectors are constructed to be orthonormal:
Lanczos vectors (4.28).
These vectors are constructed to be orthonormal:
![\begin{displaymath}
V_j^{\ast} V_j = I_j,\quad \mbox{where}\quad
V_j = \left[ \begin{array}{cccc}
v_1 & v_2 & \cdots & v_j
\end{array} \right].
\end{displaymath}](img1126.png) |
(38) |
Here, 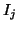 denotes the
denotes the 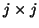 identity matrix.
In addition to (4.28), the algorithm has constructed
the vectors
identity matrix.
In addition to (4.28), the algorithm has constructed
the vectors
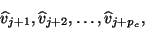 |
(39) |
which are the candidates for the next 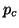 Lanczos vectors,
Lanczos vectors,
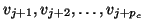 .
Here,
.
Here, 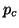 is the number of starting vectors,
is the number of starting vectors, 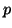 , minus
the number of deflations that have occurred during the first
, minus
the number of deflations that have occurred during the first
 iterations.
The vectors (4.30) are constructed so that they
satisfy the orthogonality relations
iterations.
The vectors (4.30) are constructed so that they
satisfy the orthogonality relations
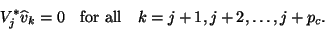 |
(40) |
The band Lanczos algorithm has a very simple built-in deflation
procedure based on the vectors (4.30).
In fact, an exact deflation at iteration 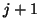 is equivalent
to
is equivalent
to
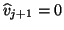 .
Therefore, in the algorithm, one checks if
.
Therefore, in the algorithm, one checks if
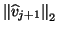 is smaller than some suitable deflation tolerance.
If yes, the vector
is smaller than some suitable deflation tolerance.
If yes, the vector 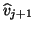 is deflated and
is deflated and 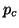 is
reduced by 1.
Otherwise,
is
reduced by 1.
Otherwise, 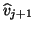 is normalized to become the next
Lanczos vector
is normalized to become the next
Lanczos vector 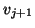 .
.
The recurrences that are used in the algorithm to generate the
vectors (4.28) and (4.30) can be summarized
compactly as follows:
![\begin{displaymath}
A V_j = V_j T_j + \left[ \begin{array}{ccccccc}
0 & \cdots ...
...hat{v}_{j+p_c}
\end{array} \right]
+ \hat{V}_j^{\rm {(dl)}}.
\end{displaymath}](img1137.png) |
(41) |
Here, 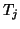 is a
is a 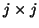 matrix whose entries are
chosen so that the orthogonality conditions (4.29)
and (4.31) are satisfied.
The matrix
matrix whose entries are
chosen so that the orthogonality conditions (4.29)
and (4.31) are satisfied.
The matrix
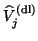 in (4.32) contains
mostly zero columns, together with the unnormalized
vectors that have been
deflated during the first
in (4.32) contains
mostly zero columns, together with the unnormalized
vectors that have been
deflated during the first  iterations.
Recall that
iterations.
Recall that 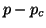 is the number of deflated vectors.
is the number of deflated vectors.
It turns out that orthogonality only has to be explicitly enforced
among 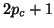 consecutive Lanczos vectors and, once deflation has
occurred, against
consecutive Lanczos vectors and, once deflation has
occurred, against 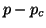 fixed earlier vectors.
As a result, the matrix
fixed earlier vectors.
As a result, the matrix 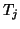 is ``essentially'' banded with
bandwidth
is ``essentially'' banded with
bandwidth 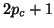 , where the bandwidth is reduced by 2 every time a
deflation occurs.
In addition, each inexact deflation causes
, where the bandwidth is reduced by 2 every time a
deflation occurs.
In addition, each inexact deflation causes 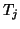 to have nonzero elements
in a fixed row outside and to the right of the banded part.
More precisely, the row index of each such row caused by deflation
is given by
to have nonzero elements
in a fixed row outside and to the right of the banded part.
More precisely, the row index of each such row caused by deflation
is given by 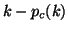 , where
, where 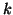 is the number of
the iteration at which the deflation has occurred and
is the number of
the iteration at which the deflation has occurred and 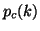 is the
corresponding value of
is the
corresponding value of 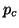 at that iteration.
The matrix
at that iteration.
The matrix 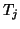 can thus be written as
can thus be written as
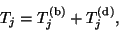 |
(42) |
where
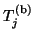 is a banded matrix and
is a banded matrix and
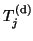 contains the horizontal ``spikes'' outside the band of
contains the horizontal ``spikes'' outside the band of 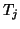 due to
deflation.
In particular, if no inexact deflation has occurred, then
due to
deflation.
In particular, if no inexact deflation has occurred, then
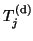 is the zero matrix.
Finally, we note that the banded part
is the zero matrix.
Finally, we note that the banded part
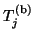 of
of 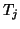 is
a Hermitian matrix.
is
a Hermitian matrix.
For example, consider the case of 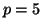 starting vectors and
assume that during the first
starting vectors and
assume that during the first 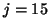 iterations, deflations
have occurred at steps
iterations, deflations
have occurred at steps 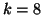 ,
, 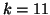 , and
, and 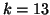 .
These three deflations correspond to deleting the vectors
.
These three deflations correspond to deleting the vectors 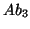 ,
,
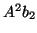 , and
, and 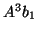 , as well as the following
, as well as the following  -multiples
of these three vectors, from the block Krylov sequence (4.27).
In this case, the matrix
-multiples
of these three vectors, from the block Krylov sequence (4.27).
In this case, the matrix
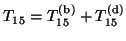 has the following sparsity structure:
has the following sparsity structure:
![\begin{displaymath}
T_{15} = %%\footnotesize{
\left[ \begin{array}{ccccccccccccc...
... \\
& & & & & & & & & & & &{*}&{*}&{*}
\end{array} \right].
\end{displaymath}](img1155.png) |
(43) |
Here, the 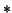 's denote potentially nonzero entries within
the banded part,
's denote potentially nonzero entries within
the banded part,
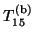 , and the
, and the 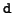 's denote
potentially nonzero entries of
's denote
potentially nonzero entries of
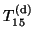 due to the deflations at iterations
due to the deflations at iterations 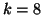 ,
, 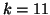 , and
, and 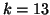 .
Note that the three deflations have reduced the initial
bandwidth
.
Note that the three deflations have reduced the initial
bandwidth 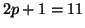 to
to 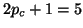 at iteration
at iteration 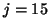 .
.
After  iterations of the band Lanczos algorithm,
approximate eigensolutions for the Hermitian
eigenvalue problem (4.25) are obtained by
computing eigensolutions of
iterations of the band Lanczos algorithm,
approximate eigensolutions for the Hermitian
eigenvalue problem (4.25) are obtained by
computing eigensolutions of
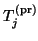 ,
,
Here,
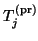 is the projection of
is the projection of  onto the space spanned by the Lanczos basis matrix
onto the space spanned by the Lanczos basis matrix 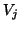 , i.e.,
, i.e.,
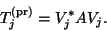 |
(44) |
Each value
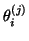 and its Ritz vector,
and its Ritz vector,
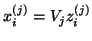 , yield an approximate eigenpair of
, yield an approximate eigenpair of  .
Of course, the matrix
.
Of course, the matrix
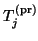 is not computed via
its definition (4.35).
Instead, we use the formula
is not computed via
its definition (4.35).
Instead, we use the formula
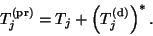 |
(45) |
By (4.36), we only have to conjugate and
transpose the part of 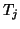 outside its banded part and add it to
outside its banded part and add it to
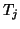 in order to obtain
in order to obtain
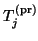 .
To show that (4.36) indeed holds true, note that
by multiplying (4.32) from the
left by
.
To show that (4.36) indeed holds true, note that
by multiplying (4.32) from the
left by 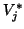 and by using the orthogonality
relations (4.29) and (4.31), we get
and by using the orthogonality
relations (4.29) and (4.31), we get
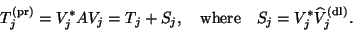 |
(46) |
Since the matrices
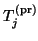 and
and
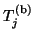 are
both Hermitian, it follows from (4.33) that
are
both Hermitian, it follows from (4.33) that
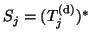 in (4.37).
Thus (4.37) reduces to (4.36).
in (4.37).
Thus (4.37) reduces to (4.36).
For example, for 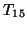 in (4.34) the associated
matrix
in (4.34) the associated
matrix
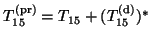 is of the form
is of the form
![\begin{displaymath}
T_{15}^{\rm {(pr)}} = %%\footnotesize{
\left[ \begin{array}{...
... &
&\overline{{\tt d}}& & &{*}&{*}&{*}
\end{array} \right].
\end{displaymath}](img1172.png) |
(47) |
Here, the
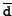 's below the banded
part were obtained by conjugating and transposing the corresponding
entries above the banded part in (4.34).
We remark that, in (4.38), the entries
's below the banded
part were obtained by conjugating and transposing the corresponding
entries above the banded part in (4.34).
We remark that, in (4.38), the entries 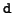 and
and
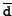 outside the banded part are usually small.
More precisely, if the deflation criterion (4.42)
below is used, then the absolute values of all
outside the banded part are usually small.
More precisely, if the deflation criterion (4.42)
below is used, then the absolute values of all 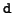 's and
's and
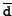 's is bounded by the deflation
tolerance
's is bounded by the deflation
tolerance 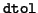 .
Even though these entries are small, setting them to zero
would introduce unnecessary errors.
Indeed, the projection property (4.35) for
.
Even though these entries are small, setting them to zero
would introduce unnecessary errors.
Indeed, the projection property (4.35) for
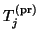 holds true only if all entries
holds true only if all entries 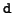 and
and
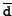 outside the banded part are included in
outside the banded part are included in
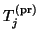 .
.
Finally, we note that the band Lanczos
algorithm terminates as soon as 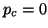 is reached.
This means that
is reached.
This means that 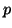 deflations have occurred, and thus the
block Krylov sequence is exhausted.
At termination due to
deflations have occurred, and thus the
block Krylov sequence is exhausted.
At termination due to 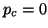 , the relation (4.32)
for the Lanczos vectors reduces to
, the relation (4.32)
for the Lanczos vectors reduces to
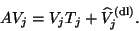 |
(48) |
Using (4.37), we can rewrite (4.39) as
follows:
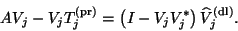 |
(49) |
Now let
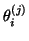 and
and 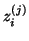 be any of the eigenpairs
of
be any of the eigenpairs
of
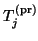 , and assume that
, and assume that 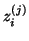 is normalized
so that
is normalized
so that
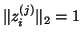 .
Recall that the pair
.
Recall that the pair
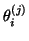 and
and
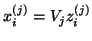 is used as an approximate eigensolution of
is used as an approximate eigensolution of  .
By multiplying (4.40) from the right by
.
By multiplying (4.40) from the right by 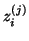 and taking norms, it follows that the residual of the
approximate eigensolution
and taking norms, it follows that the residual of the
approximate eigensolution
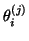 and
and 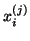 can be bounded as follows:
can be bounded as follows:
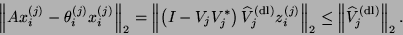 |
(50) |
In particular, if only exact deflation is performed, then
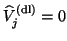 and (4.41) shows that
each eigenvalue
and (4.41) shows that
each eigenvalue
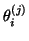 of
of
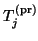 is indeed an eigenvalue of
is indeed an eigenvalue of  .
For general deflation,
.
For general deflation,
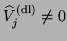 , however,
, however,
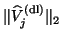 is of the order
of the deflation tolerance.
More precisely, if the deflation check (4.42) below
is used, then
is of the order
of the deflation tolerance.
More precisely, if the deflation check (4.42) below
is used, then
where 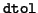 denotes the deflation tolerance.
denotes the deflation tolerance.





Next: Algorithm
Up: Band Lanczos Method
Previous: The Need for Deflation
Contents
Index
Susan Blackford
2000-11-20
![]() iterations, the band Lanczos algorithm has
generated the first
iterations, the band Lanczos algorithm has
generated the first ![]() Lanczos vectors (4.28).
These vectors are constructed to be orthonormal:
Lanczos vectors (4.28).
These vectors are constructed to be orthonormal:
![]() consecutive Lanczos vectors and, once deflation has
occurred, against
consecutive Lanczos vectors and, once deflation has
occurred, against ![]() fixed earlier vectors.
As a result, the matrix
fixed earlier vectors.
As a result, the matrix ![]() is ``essentially'' banded with
bandwidth
is ``essentially'' banded with
bandwidth ![]() , where the bandwidth is reduced by 2 every time a
deflation occurs.
In addition, each inexact deflation causes
, where the bandwidth is reduced by 2 every time a
deflation occurs.
In addition, each inexact deflation causes ![]() to have nonzero elements
in a fixed row outside and to the right of the banded part.
More precisely, the row index of each such row caused by deflation
is given by
to have nonzero elements
in a fixed row outside and to the right of the banded part.
More precisely, the row index of each such row caused by deflation
is given by ![]() , where
, where ![]() is the number of
the iteration at which the deflation has occurred and
is the number of
the iteration at which the deflation has occurred and ![]() is the
corresponding value of
is the
corresponding value of ![]() at that iteration.
The matrix
at that iteration.
The matrix ![]() can thus be written as
can thus be written as
![]() starting vectors and
assume that during the first
starting vectors and
assume that during the first ![]() iterations, deflations
have occurred at steps
iterations, deflations
have occurred at steps ![]() ,
, ![]() , and
, and ![]() .
These three deflations correspond to deleting the vectors
.
These three deflations correspond to deleting the vectors ![]() ,
,
![]() , and
, and ![]() , as well as the following
, as well as the following ![]() -multiples
of these three vectors, from the block Krylov sequence (4.27).
In this case, the matrix
-multiples
of these three vectors, from the block Krylov sequence (4.27).
In this case, the matrix
![]() has the following sparsity structure:
has the following sparsity structure:
![]() iterations of the band Lanczos algorithm,
approximate eigensolutions for the Hermitian
eigenvalue problem (4.25) are obtained by
computing eigensolutions of
iterations of the band Lanczos algorithm,
approximate eigensolutions for the Hermitian
eigenvalue problem (4.25) are obtained by
computing eigensolutions of
![]() ,
,
![]() in (4.34) the associated
matrix
in (4.34) the associated
matrix
![]() is of the form
is of the form
![]() is reached.
This means that
is reached.
This means that ![]() deflations have occurred, and thus the
block Krylov sequence is exhausted.
At termination due to
deflations have occurred, and thus the
block Krylov sequence is exhausted.
At termination due to ![]() , the relation (4.32)
for the Lanczos vectors reduces to
, the relation (4.32)
for the Lanczos vectors reduces to