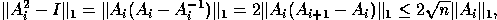Implementation and Performance on the CM-5



Next: Performance Model
Up: Implementation and Performance
Previous: Implementation and Performance
The Thinking Machines CM-5 was introduced in 1991.
The tests in this section were run on a 32 processor CM-5 at the University
of California at Berkeley.
Each CM-5 node contains a 33 MHz Sparc with an FPU and 64 KB cache,
four vector floating points units, and 32 MB of memory.
The front end is a 33 HMz Sparc with 32 MB of memory.
With the vector units, the peak 64-bit
floating point performance is 128 megaflops per node (32 megaflops per vector unit).
See [53] for more details.
Algorithm 1 was implemented
in CM Fortran (CMF) version 2.1 - an implementation of
Fortran 77 supplemented with array-processing extensions from the
ANSI and ISO (draft) standard Fortran 90 [53].
CMF arrays come in two flavors. They can be distributed
across CM processor memory (in some user defined layout)
or allocated in normal column major fashion on the front end alone.
When the front end computer executes a CM Fortran program,
it performs serial operations on scalar data stored in
its own memory, but sends any instructions for array operations
to the CM. On receiving an instruction, each node executes it on its own data.
When necessary, CM processors can access each other's memory by any of
three communication mechanisms, but these are transparent to the
CMF programmer [52].
We also used
CMSSL version 3.2, [54], TMC's library of numerical linear algebra routines.
CMSSL provides data parallel implementations of many standard linear algebra
routines, and is designed to be used with CMF and to exploit the vector units.
CMSSL's QR factorization (available with or without pivoting)
uses standard Householder transformations. Column blocking
can be performed at the user's discretion to
improve load balance and increase parallelism.
Scaling is available to avoid situations
when a column norm is close to  or
or  , but this is an expensive ``insurance policy''.
Scaling is not used in our current CM-5 code,
but should perhaps be made available in our toolbox for the informed user.
The QR with pivoting (QRP) factorization routine, which we shall use to reveal rank,
is about half as fast as QR without pivoting. This is due in part to
the elimination of blocking techniques when pivoting, as
columns must be processed sequentially.
, but this is an expensive ``insurance policy''.
Scaling is not used in our current CM-5 code,
but should perhaps be made available in our toolbox for the informed user.
The QR with pivoting (QRP) factorization routine, which we shall use to reveal rank,
is about half as fast as QR without pivoting. This is due in part to
the elimination of blocking techniques when pivoting, as
columns must be processed sequentially.
Gaussian elimination with or without partial pivoting is
available to compute LU factorizations and
perform back substitution to solve a system of equations.
Matrix inversion is performed by solving the system 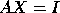 .
The LU factors can be obtained separately - to support
Balzer's and Byers' scaling schemes to accelerate the convergence of Newton,
and which require a determinant computation - and
there is a routine for estimating
.
The LU factors can be obtained separately - to support
Balzer's and Byers' scaling schemes to accelerate the convergence of Newton,
and which require a determinant computation - and
there is a routine for estimating 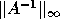 from the LU factors to detect ill-conditioning
of intermediate matrices in the Newton iteration.
Both the factorization and inversion routines balance load
by permuting the matrix, and blocking (as specified by the user) is
used to improve performance.
from the LU factors to detect ill-conditioning
of intermediate matrices in the Newton iteration.
Both the factorization and inversion routines balance load
by permuting the matrix, and blocking (as specified by the user) is
used to improve performance.
The LU, QR and Matrix multiplication routines all have ``out-of-core''
counterparts to support matrices/systems that are too
large to fit in main memory.
Our current CM5 implementation of the SDC algorithms does not
use any of the out-of-core routines, but in principle our algorithms
will permit out-of-core solutions to be used.
Figure 4 summarizes the performance of the CMSSL routines
underlying this implementation Algorithm 1.

Figure 4: Performance of some CMSSL 3.2 subroutines on 32 PEs
with VUs CM-5
We tested the Newton-Schulz iteration based algorithm
for computing the spectral decomposition along the pure imaginary axis,
since matrix multiplication can be twice as fast as matrix inversion;
see Figure 4.
The entries of random test matrices were uniformly distributed on  .
We use the inequality
.
We use the inequality 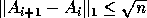 as switching
criterion from the Newton iteration (2.5) to the
Newton-Schulz iteration (2.6), i.e., we relaxed
the convergence condition
as switching
criterion from the Newton iteration (2.5) to the
Newton-Schulz iteration (2.6), i.e., we relaxed
the convergence condition 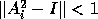 for the Newton-Schulz
iteration to
for the Newton-Schulz
iteration to
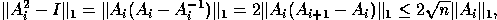
because this optimized performance over the test cases we ran.
Table 3 shows the measured results of the backward
accuracy, total CPU time and megaflops rate.
The second column of the table is the backward error, the number of
Newton iterations and the number of the Newton-Schulz iterations, respectively.
From the table, we see that by comparing to CMSSL 3.2 matrix multiplication
performance, we obtain 32% to 45% efficiency
with the matrices sizes from 512 to 2048, even faster than the
CMSSL 3.2
matrix inverse subroutine.
We profiled the total CPU time on each phase of the algorithm, and
found that about 83% of total time is spent on the Newton iteration,
9% on the QR decomposition with pivoting, and 7.5% on the matrix
multiplication for the Newton-Schulz iteration and orthogonal transformations.

Table 3: Backward accuracy, timing in seconds and megaflops of the SDC
algorithm with Newton-Schulz iteration on a 32 PEs with VUs CM-5.



Next: Performance Model
Up: Implementation and Performance
Previous: Implementation and Performance
Jack Dongarra
Mon Jan 9 11:07:50 EST 1995
 or
or  , but this is an expensive ``insurance policy''.
Scaling is not used in our current CM-5 code,
but should perhaps be made available in our toolbox for the informed user.
The QR with pivoting (QRP) factorization routine, which we shall use to reveal rank,
is about half as fast as QR without pivoting. This is due in part to
the elimination of blocking techniques when pivoting, as
columns must be processed sequentially.
, but this is an expensive ``insurance policy''.
Scaling is not used in our current CM-5 code,
but should perhaps be made available in our toolbox for the informed user.
The QR with pivoting (QRP) factorization routine, which we shall use to reveal rank,
is about half as fast as QR without pivoting. This is due in part to
the elimination of blocking techniques when pivoting, as
columns must be processed sequentially.
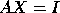 .
The LU factors can be obtained separately - to support
Balzer's and Byers' scaling schemes to accelerate the convergence of Newton,
and which require a determinant computation - and
there is a routine for estimating
.
The LU factors can be obtained separately - to support
Balzer's and Byers' scaling schemes to accelerate the convergence of Newton,
and which require a determinant computation - and
there is a routine for estimating 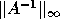 from the LU factors to detect ill-conditioning
of intermediate matrices in the Newton iteration.
Both the factorization and inversion routines balance load
by permuting the matrix, and blocking (as specified by the user) is
used to improve performance.
from the LU factors to detect ill-conditioning
of intermediate matrices in the Newton iteration.
Both the factorization and inversion routines balance load
by permuting the matrix, and blocking (as specified by the user) is
used to improve performance.

 .
We use the inequality
.
We use the inequality 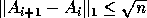 as switching
criterion from the Newton iteration (
as switching
criterion from the Newton iteration (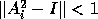 for the Newton-Schulz
iteration to
for the Newton-Schulz
iteration to