Testing




Next: Rationale
Up: Implementation
Previous: Auxiliary Subprograms.
Master test programs have been designed, developed
and included with the submitted code. This package
consists of several main programs and a set of
subprograms generating test data and comparing the
results with data obtained by element-wise
computations or the sequential BLAS. These testing
programs assume the correctness of the BLAS and the
BLACS routines; it is therefore highly recommended
to run the testing programs provided with both of
these packages before performing any PBLAS test.
A separate test program exists for each of the four
data types ( real, complex, double precision
and complex 16 ) as well as each PBLAS level.
All test programs conform to the same pattern with
only the minimum necessary changes. These programs
have been designed not merely to check whether the
model implementation has been correctly installed,
but also to serve as a validation tool and a modest
debugging aid for any specialized implementation.
16 ) as well as each PBLAS level.
All test programs conform to the same pattern with
only the minimum necessary changes. These programs
have been designed not merely to check whether the
model implementation has been correctly installed,
but also to serve as a validation tool and a modest
debugging aid for any specialized implementation.
These programs have the following features:
- the parameters of the test problems and
the names of the subprogram to be tested
are specified by means of an input data
file, which can easily be modified for
debugging,
- the data for the test problems are
generated internally and the results are
checked internally,
- the programs check that no arguments are
changed by the routines except the designated
output scalar, vector or matrix. All input
error exits (caused by illegal parameter
values) are tested,
- the programs generate a concise summary
report of the tests as well as pertinent
error messages when needed.
Input data files are supplied with every test
program, but installers and implementors must
be alert to the possible need to extend or
modify them. Values of the elements of the
matrix operands are uniformly distributed
over 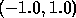 . Care is taken to ensure
that the data have full working accuracy.
Elements in the distributed matrices that
are not to be referenced by a subprogram
are either checked after exiting the routine
or set to a ``rogue'' value
. Care is taken to ensure
that the data have full working accuracy.
Elements in the distributed matrices that
are not to be referenced by a subprogram
are either checked after exiting the routine
or set to a ``rogue'' value 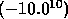 to
increase the likelihood that a reference to
them will be detected. If a computational
error is reported and an element of the
computed result is of order
to
increase the likelihood that a reference to
them will be detected. If a computational
error is reported and an element of the
computed result is of order  ,
then the routine has almost certainly
referenced the wrong element of the array.
,
then the routine has almost certainly
referenced the wrong element of the array.
After each call to a subprogram being tested,
its operation is checked in two ways. First,
each of its input arguments, including all
elements of the distributed operands, is
checked to see if it has been altered by
the subprogram. If any argument, other
than the specified elements of the result
scalar, vector or matrix, has been modified,
an error is reported. This check includes
the supposedly unreferenced elements of the
distributed matrices. Second, the resulting
scalar, vector or matrix computed by the
subprogram is compared with the corresponding
result obtained by the sequential BLAS or by
simple Fortran code. We do not expect exact
agreement because the two results are not
necessarily computed by the same sequences
of floating point operations. We do, however,
expect the differences to be small relative
to working precision. The error bounds are
then the same as the ones used in the BLAS
testers. A more detailed description of
those tests can be found in [12][11].
The test ratio is determined by scaling these
error bounds by the inverse of machine epsilon
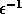 . This ratio is compared with
a constant threshold value defined in the input
data file. Test ratios greater than the
threshold are flagged as ``suspect''.
On the basis of the BLAS experience a
threshold value of 16 is recommended. The precise
value is not critical. Errors in the routines
are most likely to be errors in array indexing,
which will almost certainly lead to a totally
wrong result. A more subtle potential error is
the use of a single precision variable in a
double precision computation. This is likely
to lead to a loss of half the machine epsilon.
The test programs regard a test ratio greater
than
. This ratio is compared with
a constant threshold value defined in the input
data file. Test ratios greater than the
threshold are flagged as ``suspect''.
On the basis of the BLAS experience a
threshold value of 16 is recommended. The precise
value is not critical. Errors in the routines
are most likely to be errors in array indexing,
which will almost certainly lead to a totally
wrong result. A more subtle potential error is
the use of a single precision variable in a
double precision computation. This is likely
to lead to a loss of half the machine epsilon.
The test programs regard a test ratio greater
than 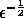 as an error.
as an error.
The PBLAS testing programs are thus very similar
to what has been done for the BLAS. However, it
was necessary to slightly depart from the way
the BLAS testing programs operate due to the
difficulties inherent to the testing of programs
written for distributed-memory computers.
The first obstacle is due to the significant
increase of testing parameters. Indeed,
programs for distributed-memory computers
need to be tested for virtually any number
of processes. Moreover, it should also be
possible to vary the data distribution
parameters such as the block sizes defined
in Sect. 3.2.
These facts motivated the decision to permit
a user configurable set of tests for every
routine. Consequently, one can test the
PBLAS with any possible machine configuration
as well as data layout.
The second more subtle difficulty is due to the
routines producing an output scalar such as
P NRM2. Because of the block-cyclic
decomposition properties and the fact that vector
operands are so far restricted to a matrix row or
column, it follows that only one process row or
column will own the input vector. This process row
or column is subsequently called the vector scope
by analogy with the BLACS terminology. The question
becomes: which processes should get the correct
result ? It experimentally appeared convenient
to broadcast the result to every process in the
vector scope only and set it to zero elsewhere.
If this scalar is needed by every process in
the grid, it is the user's responsibility to
broadcast it. Consequently, such routines need
only to be called by the processes in the vector
scope. Moreover, this appropriate specification
to what is needed by the ScaLAPACK routines
introduces a slight ambiguity when one wants
to compute for example the norm of a column of
a 1-by-N distributed matrix. Indeed,
this 1-column can equivalently be seen as a
row subsection containing one entry. In
practice, this case rarely occurs. Should it
happen, the PBLAS routines return the correct
result only in the process owning the input
vector operand and zero in every other grid
process.
NRM2. Because of the block-cyclic
decomposition properties and the fact that vector
operands are so far restricted to a matrix row or
column, it follows that only one process row or
column will own the input vector. This process row
or column is subsequently called the vector scope
by analogy with the BLACS terminology. The question
becomes: which processes should get the correct
result ? It experimentally appeared convenient
to broadcast the result to every process in the
vector scope only and set it to zero elsewhere.
If this scalar is needed by every process in
the grid, it is the user's responsibility to
broadcast it. Consequently, such routines need
only to be called by the processes in the vector
scope. Moreover, this appropriate specification
to what is needed by the ScaLAPACK routines
introduces a slight ambiguity when one wants
to compute for example the norm of a column of
a 1-by-N distributed matrix. Indeed,
this 1-column can equivalently be seen as a
row subsection containing one entry. In
practice, this case rarely occurs. Should it
happen, the PBLAS routines return the correct
result only in the process owning the input
vector operand and zero in every other grid
process.
Finally, there are special challenges associated
with writing and testing numerical software to be
executed on networks containing heterogeneous
processors [4], i.e., processors which
perform floating point arithmetic differently.
This includes not just machines with different
floating point formats and semantics such as
Cray computers and workstations performing IEEE
standard floating point arithmetic, but even
supposedly identical machines running different
compilers or even just different compiler options.
Moreover, on such networks, floating point data
transfers between two processes may require a
data conversion phase and thus a possible loss
of accuracy. It is therefore impractical,
error-prone and difficult to compare supposedly
identical computed scalars on such heterogeneous
networks. As a consequence, the validity and
correctness of the tests performed can only be
guaranteed for networks of processors with
identical floating point formats.




Next: Rationale
Up: Implementation
Previous: Auxiliary Subprograms.
Jack Dongarra
Thu Aug 3 07:53:00 EDT 1995
 16 ) as well as each PBLAS level.
All test programs conform to the same pattern with
only the minimum necessary changes. These programs
have been designed not merely to check whether the
model implementation has been correctly installed,
but also to serve as a validation tool and a modest
debugging aid for any specialized implementation.
16 ) as well as each PBLAS level.
All test programs conform to the same pattern with
only the minimum necessary changes. These programs
have been designed not merely to check whether the
model implementation has been correctly installed,
but also to serve as a validation tool and a modest
debugging aid for any specialized implementation.
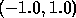 . Care is taken to ensure
that the data have full working accuracy.
Elements in the distributed matrices that
are not to be referenced by a subprogram
are either checked after exiting the routine
or set to a ``rogue'' value
. Care is taken to ensure
that the data have full working accuracy.
Elements in the distributed matrices that
are not to be referenced by a subprogram
are either checked after exiting the routine
or set to a ``rogue'' value 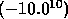 to
increase the likelihood that a reference to
them will be detected. If a computational
error is reported and an element of the
computed result is of order
to
increase the likelihood that a reference to
them will be detected. If a computational
error is reported and an element of the
computed result is of order  ,
then the routine has almost certainly
referenced the wrong element of the array.
,
then the routine has almost certainly
referenced the wrong element of the array.
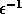 . This ratio is compared with
a constant threshold value defined in the input
data file. Test ratios greater than the
threshold are flagged as ``suspect''.
On the basis of the BLAS experience a
threshold value of 16 is recommended. The precise
value is not critical. Errors in the routines
are most likely to be errors in array indexing,
which will almost certainly lead to a totally
wrong result. A more subtle potential error is
the use of a single precision variable in a
double precision computation. This is likely
to lead to a loss of half the machine epsilon.
The test programs regard a test ratio greater
than
. This ratio is compared with
a constant threshold value defined in the input
data file. Test ratios greater than the
threshold are flagged as ``suspect''.
On the basis of the BLAS experience a
threshold value of 16 is recommended. The precise
value is not critical. Errors in the routines
are most likely to be errors in array indexing,
which will almost certainly lead to a totally
wrong result. A more subtle potential error is
the use of a single precision variable in a
double precision computation. This is likely
to lead to a loss of half the machine epsilon.
The test programs regard a test ratio greater
than 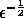 as an error.
as an error.
 NRM2. Because of the block-cyclic
decomposition properties and the fact that vector
operands are so far restricted to a matrix row or
column, it follows that only one process row or
column will own the input vector. This process row
or column is subsequently called the vector scope
by analogy with the BLACS terminology. The question
becomes: which processes should get the correct
result ? It experimentally appeared convenient
to broadcast the result to every process in the
vector scope only and set it to zero elsewhere.
If this scalar is needed by every process in
the grid, it is the user's responsibility to
broadcast it. Consequently, such routines need
only to be called by the processes in the vector
scope. Moreover, this appropriate specification
to what is needed by the ScaLAPACK routines
introduces a slight ambiguity when one wants
to compute for example the norm of a column of
a 1-by-N distributed matrix. Indeed,
this 1-column can equivalently be seen as a
row subsection containing one entry. In
practice, this case rarely occurs. Should it
happen, the PBLAS routines return the correct
result only in the process owning the input
vector operand and zero in every other grid
process.
NRM2. Because of the block-cyclic
decomposition properties and the fact that vector
operands are so far restricted to a matrix row or
column, it follows that only one process row or
column will own the input vector. This process row
or column is subsequently called the vector scope
by analogy with the BLACS terminology. The question
becomes: which processes should get the correct
result ? It experimentally appeared convenient
to broadcast the result to every process in the
vector scope only and set it to zero elsewhere.
If this scalar is needed by every process in
the grid, it is the user's responsibility to
broadcast it. Consequently, such routines need
only to be called by the processes in the vector
scope. Moreover, this appropriate specification
to what is needed by the ScaLAPACK routines
introduces a slight ambiguity when one wants
to compute for example the norm of a column of
a 1-by-N distributed matrix. Indeed,
this 1-column can equivalently be seen as a
row subsection containing one entry. In
practice, this case rarely occurs. Should it
happen, the PBLAS routines return the correct
result only in the process owning the input
vector operand and zero in every other grid
process.