
The communication pattern of a set of processes can be represented by a graph. The nodes stand for the processes, and the edges connect processes that communicate with each other. Since communication is most often symmetric, communication graphs are assumed to be symmetric: if an edge uv connects node u to node v , then an edge uv connects node v to node u .
MPI provides message-passing between any pair of processes in a group. There is no requirement for opening a channel explicitly. Therefore, a ``missing link'' in the user-defined process graph does not prevent the corresponding processes from exchanging messages. It means, rather, that this connection is neglected in the virtual topology. This strategy implies that the topology gives no convenient way of naming this pathway of communication. Another possible consequence is that an automatic mapping tool (if one exists for the runtime environment) will not take account of this edge when mapping, and communication on the ``missing'' link will be less efficient.

Specifying the virtual topology in terms of a graph is sufficient for all applications. However, in many applications the graph structure is regular, and the detailed set-up of the graph would be inconvenient for the user and might be less efficient at run time. A large fraction of all parallel applications use process topologies like rings, two- or higher-dimensional grids, or tori. These structures are completely defined by the number of dimensions and the numbers of processes in each coordinate direction. Also, the mapping of grids and tori is generally an easier problem than general graphs. Thus, it is desirable to address these cases explicitly.
Process coordinates in a Cartesian structure begin their numbering at 0.
Row-major numbering is always used for the processes in a
Cartesian structure. This means that, for example, the relation
between group rank and coordinates for twelve processes in
a 3x4 grid is as shown in Figure ![]() .
.
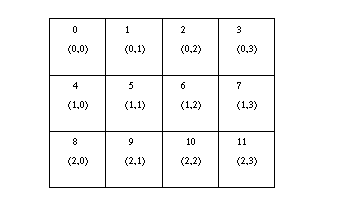
Figure: Relationship between ranks and Cartesian coordinates for a
3x4 2D topology. The upper number in each box is the rank of the process
and the lower value is the (row, column) coordinates.