Cholesky Factorization



Next: Performance Results
Up: Factorization Routines
Previous: QR Factorization
Cholesky factorization factors an 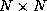 , symmetric, positive-definite
matrix
, symmetric, positive-definite
matrix 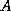 into
the product of a lower triangular matrix
into
the product of a lower triangular matrix 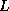 and its transpose, i.e.,
and its transpose, i.e.,
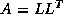 (or
(or 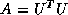 , where
, where 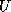 is upper triangular).
It is assumed that the lower triangular portion of
is upper triangular).
It is assumed that the lower triangular portion of 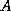 is stored
in the lower triangle of a two-dimensional array
and that the computed elements of
is stored
in the lower triangle of a two-dimensional array
and that the computed elements of 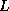 overwrite the given elements of
overwrite the given elements of 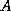 .
At the
.
At the  -th step, we partition the
-th step, we partition the 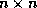 matrices
matrices 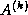 ,
, 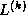 ,
and
,
and  , and write the system as
, and write the system as
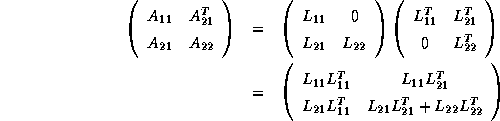
where the block 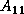 is
is 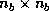 ,
, 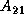 is
is 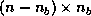 ,
and
,
and 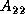 is
is  .
.
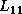 and
and 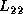 are lower triangular.
are lower triangular.
The block-partitioned form of
Cholesky factorization may be inferred inductively as follows.
If we assume that 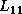 , the lower triangular Cholesky factor
of
, the lower triangular Cholesky factor
of 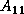 , is known, we can rearrange the block equations,
, is known, we can rearrange the block equations,

A snapshot of the block Cholesky factorization algorithm in
Figure 5 shows
how the column panel 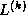 (
(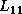 and
and 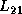 ) is computed
and how the trailing submatrix
) is computed
and how the trailing submatrix 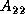 is updated.
The factorization can be done by recursively applying the steps
outlined above to the
is updated.
The factorization can be done by recursively applying the steps
outlined above to the  matrix
matrix 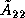 .
.
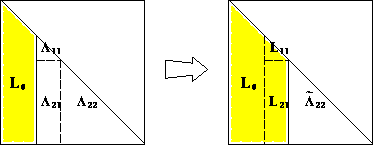
Figure 5:
A snapshot of block Cholesky factorization.
In the right-looking version of the LAPACK routine,
the computation of the above steps involves the following operations:
-
DPOTF2: Compute the Cholesky factorization of the diagonal block
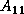 .
.
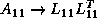
-
DTRSM: Compute the column panel
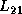 ,
,

-
DSYRK: Update the rest of the matrix,
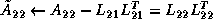
The parallel implementation of the corresponding ScaLAPACK routine,
PDPOTRF, proceeds as follows:
-
PDPOTF2:
The process
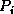 , which has the
, which has the 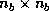 diagonal block
diagonal block 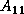 ,
performs the Cholesky factorization of
,
performs the Cholesky factorization of 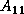 .
.
-
PDTRSM:
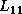 is broadcast columnwise by
is broadcast columnwise by 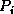 down all rows in
the current column of processes, which
computes the column of blocks of
down all rows in
the current column of processes, which
computes the column of blocks of 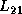 .
.
-
PDSYRK: the column of blocks
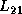 is broadcast rowwise across
all columns of processes and then transposed.
Now, processes have their own portions of
is broadcast rowwise across
all columns of processes and then transposed.
Now, processes have their own portions of 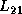 and
and 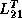 .
They update their local portions of the matrix
.
They update their local portions of the matrix 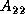 .
.



Next: Performance Results
Up: Factorization Routines
Previous: QR Factorization
Susan Ostrouchov
Fri Apr 28 09:37:26 EDT 1995
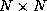 , symmetric, positive-definite
matrix
, symmetric, positive-definite
matrix 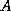 into
the product of a lower triangular matrix
into
the product of a lower triangular matrix 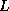 and its transpose, i.e.,
and its transpose, i.e.,
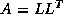 (or
(or 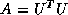 , where
, where 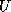 is upper triangular).
It is assumed that the lower triangular portion of
is upper triangular).
It is assumed that the lower triangular portion of 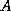 is stored
in the lower triangle of a two-dimensional array
and that the computed elements of
is stored
in the lower triangle of a two-dimensional array
and that the computed elements of 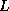 overwrite the given elements of
overwrite the given elements of 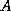 .
At the
.
At the  -th step, we partition the
-th step, we partition the 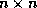 matrices
matrices 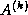 ,
, 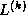 ,
and
,
and  , and write the system as
, and write the system as
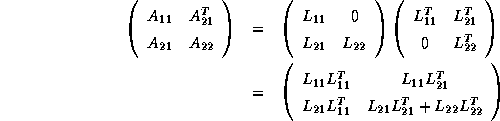
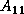 is
is 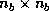 ,
, 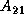 is
is 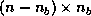 ,
and
,
and 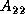 is
is  .
.
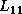 and
and 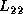 are lower triangular.
are lower triangular.

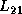 ) is computed
and how the trailing submatrix
) is computed
and how the trailing submatrix 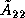 .
.

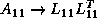

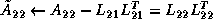
 , which has the
, which has the 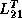 .
They update their local portions of the matrix
.
They update their local portions of the matrix