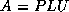 ,
where
,
where 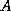 and
and 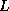 are
are 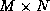 matrices, and
matrices, and 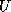 is an
is an
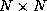 matrix.
matrix. 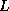 is unit lower triangular (lower triangular with
1's on the main diagonal),
is unit lower triangular (lower triangular with
1's on the main diagonal), 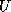 is upper triangular, and
is upper triangular, and
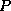 is a permutation matrix, which is stored in a
is a permutation matrix, which is stored in a 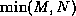 vector.
vector.
The LU factorization applies a sequence of Gaussian eliminations
to form 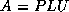 ,
where
,
where 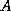 and
and 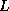 are
are 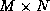 matrices, and
matrices, and 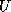 is an
is an
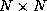 matrix.
matrix. 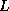 is unit lower triangular (lower triangular with
1's on the main diagonal),
is unit lower triangular (lower triangular with
1's on the main diagonal), 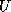 is upper triangular, and
is upper triangular, and
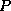 is a permutation matrix, which is stored in a
is a permutation matrix, which is stored in a 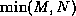 vector.
vector.
At the  -th step of the computation (
-th step of the computation (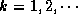 ), it is assumed that
the
), it is assumed that
the 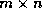 submatrix of
submatrix of 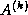 (
(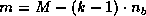 ,
,
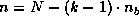 ) is to be partitioned as follows,
) is to be partitioned as follows,
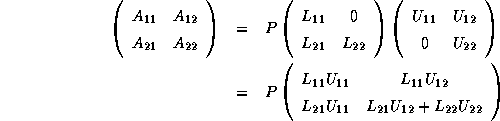
where the block 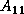 is
is 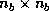 ,
, 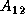 is
is 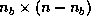 ,
,
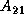 is
is 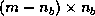 , and
, and 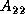 is
is 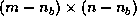 .
.
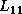 is a unit lower triangular matrix, and
is a unit lower triangular matrix, and
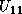 is an upper triangular matrix.
is an upper triangular matrix.
At first, a sequence of Gaussian eliminations is performed on the first
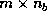 panel of
panel of 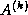 (i.e.,
(i.e., 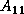 and
and 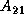 ).
Once this is completed, the matrices
).
Once this is completed, the matrices 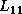 ,
, 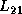 , and
, and
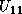 are known, and we can rearrange the block equations,
are known, and we can rearrange the block equations,
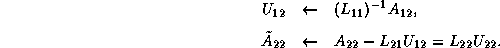
The LU factorization can be done by recursively applying the steps
outlined above to the 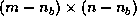 matrix
matrix 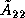 .
Figure 3 shows a snapshot of the block LU factorization.
It shows how the column panel,
.
Figure 3 shows a snapshot of the block LU factorization.
It shows how the column panel, 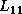 and
and 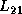 , and the row panel,
, and the row panel,
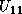 and
and 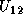 , are computed, and how the trailing submatrix
, are computed, and how the trailing submatrix 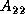 is updated. In the figure,
the shaded areas represent data for which the corresponding computations
are completed.
Later, row interchanges will be applied to
is updated. In the figure,
the shaded areas represent data for which the corresponding computations
are completed.
Later, row interchanges will be applied to 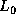 and
and 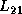 .
.
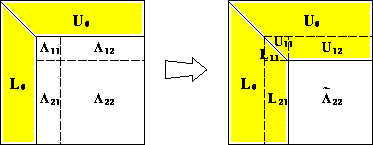
Figure 3: A snapshot of block LU factorization.
The computation of the above steps in the LAPACK routine, DGETRF, involves the following operations:
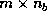 column
panel of
column
panel of 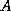 (i.e.,
(i.e., 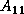 and
and 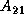 ).
).
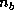 times (
times (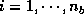 ) ]
) ]
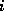 -th column and its location
-th column and its location
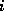 -th row with the row which
holds the maximum
-th row with the row which
holds the maximum
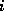 -th column of the matrix
-th column of the matrix
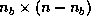 row panel of
row panel of 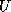 ,
,
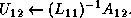
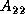 ,
,
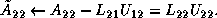
The corresponding parallel implementation of the ScaLAPACK routine, PDGETRF, proceeds as follows:
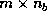 panel of
panel of 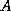 (i.e.,
(i.e., 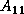 and
and 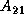 ).
).
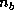 times (
times (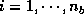 ) ]
) ]
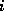 -th column and
its location (pivot information will be stored on the column of processes)
-th column and
its location (pivot information will be stored on the column of processes)
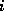 -th row with the row which holds the maximum
-th row with the row which holds the maximum
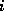 -th column of the matrix
-th column of the matrix
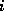 -th row columnwise (
-th row columnwise (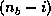 elements)
in the current column of processes and update the trailing submatrix
elements)
in the current column of processes and update the trailing submatrix
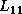 is broadcast along the current row of processes,
which converts the row panel
is broadcast along the current row of processes,
which converts the row panel 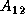 to
to 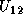 .
.
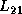 is broadcast rowwise across all
columns of processes. The row panel
is broadcast rowwise across all
columns of processes. The row panel 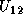 is broadcast columnwise
down all rows of processes.
Then, all processes update their local portions of the matrix,
is broadcast columnwise
down all rows of processes.
Then, all processes update their local portions of the matrix, 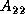 .
.