A Procedure for Choosing the Tiling Basis

In this section, we describe a practical procedure for choosing a tiling basis A\ given the dependence matrix D. The procedure's complexity is a function of k, the nesting depth of the loop; m, the number of dependence directions; and p, the number of rays of the cone . (We define what we mean by the rays of a polygonal cone below.) In these terms, the complexity of the procedure is . While the exponential term here may be cause for some uneasiness, the reader should keep in mind that in the practical application of these ideas k will rarely exceed four.

The procedure can be described as follows:

1. Construct the set of rays of the cone . A ray is a vector that is on the boundary of and is at the intersection of at least k-1 of the half spaces . Thus, the rays satisfy
 
where is a subset of the integers . This is a necessary condition. Let us suppose that there is a unique integer solution (up to scaling) of equation (6). For the solution r to be a ray, we must check whether . We also check to see whether because, if that is the case, then -r is a ray of . If we find that the rows of D selected by are linearly dependent so that (6) has a two or more dimensional subspace of solutions, then we just ignore the set .

The method we use for the construction is simply to form all of the 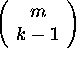subsets and then solve (6) for r. Our implementation uses a QR factorization with column pivoting, which is very effective at detecting linear dependence of the columns  [10]. It is straightforward to find the integer solution to (6) by computing a solution in floating-point and then finding the smallest scalar multiple that makes the solution integer (after perturbations on the order of roundoff error). Implementations that use only integer arithmetic would also be feasible and perhaps better.

The complexity of these decompositions is . However, we may update the QR decomposition after changing one column of the matrix at cost . Bischof has recently shown how to do so and still monitor the linear independence of columns [2]. In our experiments, we do not use such an updating procedure.

We must consider the case in which itself has a nontrivial null space, which in fact happens quite often. In this case, the set is a wedge,

where is the null space of and is the intersection of with the orthogonal complement of , the row space of . To detect this case, we always start with a QR factorization of itself. This allows us to find the rank of D and an integer basis for the null space of in a standard manner. We then construct the rays of by applying a variant of the procedure above to the augmented matrix [D, N], where the columns of N are the computed basis for . In the variant, the subsets always include all of the columns of N, and enough other columns to make up a set of k-1. The resulting rays must therefore be members of ; together with the columns of N they are the of rays of .

  
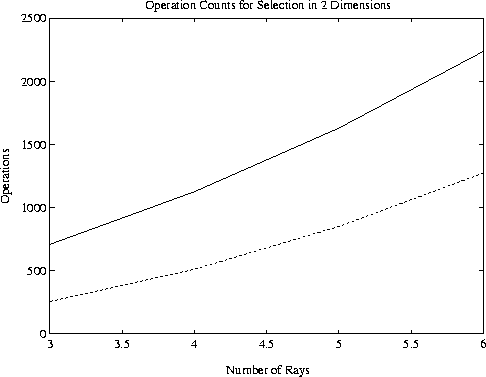
Figure 2: Operation counts versus number of rays for selection in 2 dimensions. Solid line: Subset selection; Broken line: Exhaustive search.

Having obtained the rays as the columns of a matrix , we next choose as our first approximation to the optimal basis a subset of these rays. As the cone is invariant under scaling of these rays, we normalize them so that their length is one. Then we select a subset of k of them, chosen to approximately minimize the condition number of the subset. (We show below that this also results in a nearly maximum determinant.) This is a standard problem, called subset selection, in statistics. We employ the heuristic procedure of Golub, Klema, and Stewart [9], which is described in the text of Golub and Van Loan [10]. This procedure involves a singular value decomposition (SVD) of R and the QR decomposition with column pivoting of a matrix that is part of the SVD, with an overall cost of floating-point operations (and operation being a floating-point addition and a floating-point multiplication).

  
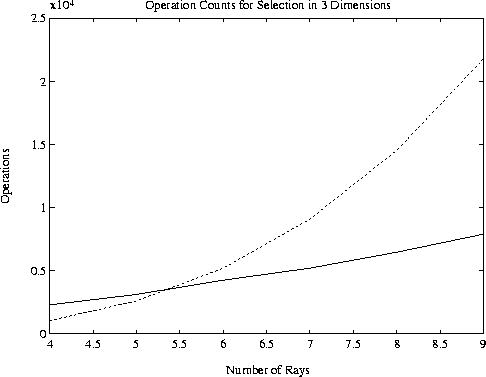
Figure 3: Operation counts versus number of rays for selection in 3 dimensions. Solid line: Subset selection; Broken line: Exhaustive search.

We know of no method for finding the optimal subset of rays other than an exhaustive search, at a cost of 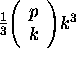flops. The relative costs of our implementation and exhaustive search for the optimum subset are illustrated in Figures 2 --  4. Obviously, the exhaustive procedure is prohibitively expensive for large problems, but may be used for k = 2, for k = 3 and p < 6, and for k = 4 and p < 6. On the other hand, subset selection does very well. In a test of 1000 randomly generated matrices D, subset selection produced a suboptimal choice in 18 cases. In the worst of these, the determinant of the basis that it found was 17% smaller than that of the optimum basis.

  
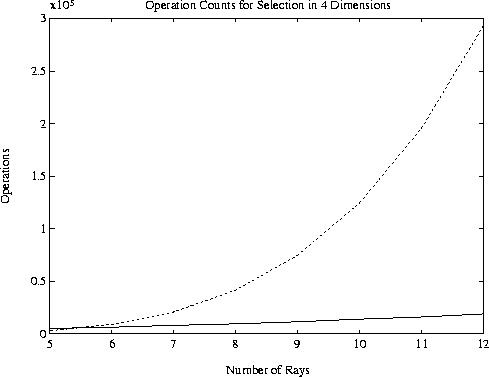
Figure 4: Operation counts versus number of rays for selection in 4 dimensions. Solid line: Subset selection; Broken line: Exhaustive search.

The basis chosen at this point may be far from optimal. Consider the case

The two rays of the cone are the columns of

These rays make an angle of ; clearly there are orthogonal bases whose elements are in , but not all at the boundaries. To catch cases like this, we have implemented a generalized orthogonalization process. Let angle(x, y) denote the angle between the vectors x and y, given by

The procedure is

 mmmmmmmmmmmmmmmmmm¯

		for j = 1 to k do  

				Find  such that angle is maximum; 

				if angle  

						

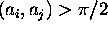
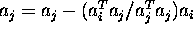
								so that  is orthogonal to ;

						Replace  with an integer vector in 

								of approximately the same direction; fi

				od   

		if  and the normalized determinant is larger than before

				improvement, accept the new , else use the old one; fi 

In a test of 1000 randomly generated dependence matrices D, the basis selected by finding the rays of and then using the subset selection procedure above was improved by this procedure. The average determinant was improved , from .63 to .71 . In comparisons with several similar procedures, this one did the best job of maximizing the normalized determinant. We also considered the following variants:

1. As above, but replace rather than after making it orthogonal to .
2. For j = 1 to k, is made orthogonal to each other basis vector with which it makes an obtuse angle; this continues until there are no such obtuse angles involving .
3. For every pair of basis vectors and with i < j, orthogonalize and by adding a multiple of to .
4. For every pair of basis vectors , and with i < j, orthogonalize and by adding a multiple of to .

Procedures 2, 3, and 4 are more costly with little in the way of improved performance. Procedure 1 actually does worse. Thus, we recommend the use of the procedure above.