




Next: 6.3.4 Physics Results
Up: Magnetism in the
Previous: 6.3.2 The Computational Algorithm
The fairly large three-dimensional lattices (usually 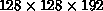 ) are partitioned into a ring of M processors with
x-dimension which is uniformly distributed among the M processors.
The local updates are easily parallelized since the connection is, at
most, next-nearest neighbor (for the time-loop update). The needed
spin-word arrays from its neighbor are copied into the local storage by
the shift routine in the CrOS communication system
[Fox:88a] before doing the update. One of the global updates, the
time line, can also be done in the same fashion. The communication is
very efficient in the sense that a single communication shift,
) are partitioned into a ring of M processors with
x-dimension which is uniformly distributed among the M processors.
The local updates are easily parallelized since the connection is, at
most, next-nearest neighbor (for the time-loop update). The needed
spin-word arrays from its neighbor are copied into the local storage by
the shift routine in the CrOS communication system
[Fox:88a] before doing the update. One of the global updates, the
time line, can also be done in the same fashion. The communication is
very efficient in the sense that a single communication shift,
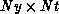 , spins instead of Nt spins in the case where the
lattice is partitioned into a two-dimensional grid. The
overhead/latency associated with the communication is thus
significantly reduced.
, spins instead of Nt spins in the case where the
lattice is partitioned into a two-dimensional grid. The
overhead/latency associated with the communication is thus
significantly reduced.
The winding-line global update along the x-direction is difficult to do in
this fashion, because it involves spins on all the M nodes. In addition,
we need to compute the correlation functions which have the same difficulty.
However, since these operations are not used very often, we devised a fairly
elegant way to parallelize these global operations. A set of
gather-scatter routines, based on the cread and cwrite in
CrOS, is written. In gather, the subspaces on each node are gathered
into complete spaces on each node, preserving the original geometric
connection. Parallelism is achieved now since the global operations are done
on each node just as in the sequential computer, with each node only doing
the part it originally covers. In scatter, the updated (changed)
lattice configuration on a particular node (number zero) is scattered
(distributed) back to all the nodes in the ring, exactly according to the
original partition. Note that this scheme differs from the earlier
decomposition scheme [Fox:84a] for the gravitation problem, where memory
size constraint is the main concern.
The hypercube nodes were divided into several independent rings,
each ring holding an independent simulation, as shown in
Figure 6.8. At higher temperatures, a spin system of
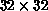 is enough, so that we can simulate several independent systems
at the same time. At low temperatures, one needs larger systems, such as
is enough, so that we can simulate several independent systems
at the same time. At low temperatures, one needs larger systems, such as
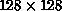 -all the nodes will then be dedicated to a single large
system. This simple parallelism makes the simulation very flexible and
efficient. In the simulation, we used a parallel version of the Fibonacci
additive random numbers generator [Ding:88d],
which has a period larger that
-all the nodes will then be dedicated to a single large
system. This simple parallelism makes the simulation very flexible and
efficient. In the simulation, we used a parallel version of the Fibonacci
additive random numbers generator [Ding:88d],
which has a period larger that 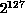 .
.
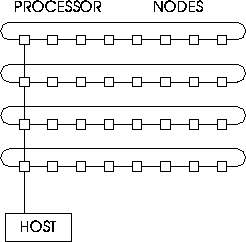
Figure 6.8: The Configuration of the Hypercube Nodes. In the example, 32
nodes are configured as four independent rings, each consisting of 8
nodes. Each ring does an independent simulation.
We have made a systematic performance analysis by running the code on
different sizes and different numbers of nodes. The timing results
for a realistic situation (20 sweeps of update, one measurement) are measured
[Ding:90k]. The speedup, 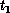 /
/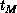 , where
, where 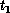 (
(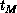 ) is the
time for the same size spins system to run same number operations on one
) is the
time for the same size spins system to run same number operations on one
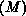 node, is plotted in Figure 6.9. One can see that speedup
is quite close to the ideal case, denoted by the dashed line. For the
node, is plotted in Figure 6.9. One can see that speedup
is quite close to the ideal case, denoted by the dashed line. For the
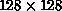 quantum spin system, the 32-node hypercube speeds up
the computation by a factor of 26.6, which is a very good result. However,
running the same spin system on a 16-node is more efficient, because we can
run two independent systems on the 32-node hypercube with a total speedup
of
quantum spin system, the 32-node hypercube speeds up
the computation by a factor of 26.6, which is a very good result. However,
running the same spin system on a 16-node is more efficient, because we can
run two independent systems on the 32-node hypercube with a total speedup
of 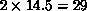 (each speedup a factor 14.5). This is better described
by efficiency, defined as speedup/nodes, which is plotted in
Figure 6.10. Clearly, the efficiency of the implementation is very
high, generally over 90%.
(each speedup a factor 14.5). This is better described
by efficiency, defined as speedup/nodes, which is plotted in
Figure 6.10. Clearly, the efficiency of the implementation is very
high, generally over 90%.
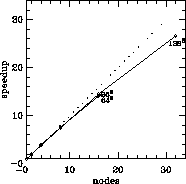
Figure 6.9: Speedup of the Parallel Algorithm for Lattice Systems 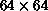 ,
, 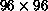 and
and 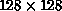 . The dashed line is the ideal
case.
. The dashed line is the ideal
case.
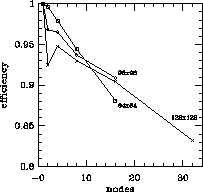
Figure 6.10: Efficiency of the Parallel Algorithm
Comparison with other supercomputers is interesting. For this
program, the one-head CRAY X-MP speed is
approximately that of a 2-node Mark IIIfp. This indicates that our
32-node Mark IIIfp performs better than the
CRAY X-MP by about a factor of 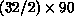 % = 14! We note that
our code is written in C and the vectorization is limited to the 32-bit
inside the words. Rewriting the code in Fortran (Fortran compilers on
the CRAY are more efficient) and fully vectorizing the code, one may
gain a factor of about three on the CRAY. Nevertheless, this quantum
Monte Carlo code is clearly a good example, in that parallel computers
easily (i.e., at same programming level) outperform the conventional
supercomputers.
% = 14! We note that
our code is written in C and the vectorization is limited to the 32-bit
inside the words. Rewriting the code in Fortran (Fortran compilers on
the CRAY are more efficient) and fully vectorizing the code, one may
gain a factor of about three on the CRAY. Nevertheless, this quantum
Monte Carlo code is clearly a good example, in that parallel computers
easily (i.e., at same programming level) outperform the conventional
supercomputers.





Next: 6.3.4 Physics Results
Up: Magnetism in the
Previous: 6.3.2 The Computational Algorithm
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
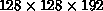 ) are partitioned into a ring of M processors with
x-dimension which is uniformly distributed among the M processors.
The local updates are easily parallelized since the connection is, at
most, next-nearest neighbor (for the time-loop update). The needed
spin-word arrays from its neighbor are copied into the local storage by
the shift routine in the CrOS communication system
[Fox:88a] before doing the update. One of the global updates, the
time line, can also be done in the same fashion. The communication is
very efficient in the sense that a single communication shift,
) are partitioned into a ring of M processors with
x-dimension which is uniformly distributed among the M processors.
The local updates are easily parallelized since the connection is, at
most, next-nearest neighbor (for the time-loop update). The needed
spin-word arrays from its neighbor are copied into the local storage by
the shift routine in the CrOS communication system
[Fox:88a] before doing the update. One of the global updates, the
time line, can also be done in the same fashion. The communication is
very efficient in the sense that a single communication shift,
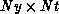 , spins instead of Nt spins in the case where the
lattice is partitioned into a two-dimensional grid. The
overhead/latency associated with the communication is thus
significantly reduced.
, spins instead of Nt spins in the case where the
lattice is partitioned into a two-dimensional grid. The
overhead/latency associated with the communication is thus
significantly reduced.





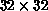 is enough, so that we can simulate several independent systems
at the same time. At low temperatures, one needs larger systems, such as
is enough, so that we can simulate several independent systems
at the same time. At low temperatures, one needs larger systems, such as
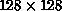 -all the nodes will then be dedicated to a single large
system. This simple parallelism makes the simulation very flexible and
efficient. In the simulation, we used a parallel version of the Fibonacci
additive random numbers
-all the nodes will then be dedicated to a single large
system. This simple parallelism makes the simulation very flexible and
efficient. In the simulation, we used a parallel version of the Fibonacci
additive random numbers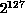 .
.

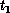 /
/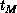 , where
, where 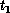 (
(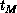 ) is the
time for the same size spins system to run same number operations on one
) is the
time for the same size spins system to run same number operations on one
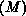 node, is plotted in Figure
node, is plotted in Figure 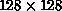 quantum spin system, the 32-node hypercube speeds up
the computation by a factor of 26.6, which is a very good result. However,
running the same spin system on a 16-node is more efficient, because we can
run two independent systems on the 32-node hypercube with a total speedup
of
quantum spin system, the 32-node hypercube speeds up
the computation by a factor of 26.6, which is a very good result. However,
running the same spin system on a 16-node is more efficient, because we can
run two independent systems on the 32-node hypercube with a total speedup
of 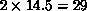 (each speedup a factor 14.5). This is better described
by efficiency, defined as speedup/nodes, which is plotted in
Figure
(each speedup a factor 14.5). This is better described
by efficiency, defined as speedup/nodes, which is plotted in
Figure 
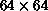 ,
, 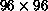 and
and 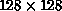 . The dashed line is the ideal
case.
. The dashed line is the ideal
case.
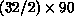 % = 14! We note that
our code is written in C and the vectorization is limited to the 32-bit
inside the words. Rewriting the code in Fortran (Fortran compilers on
the CRAY are more efficient) and fully vectorizing the code, one may
gain a factor of about three on the CRAY. Nevertheless, this quantum
Monte Carlo code is clearly a good example, in that parallel computers
easily (i.e., at same programming level) outperform the conventional
supercomputers.
% = 14! We note that
our code is written in C and the vectorization is limited to the 32-bit
inside the words. Rewriting the code in Fortran (Fortran compilers on
the CRAY are more efficient) and fully vectorizing the code, one may
gain a factor of about three on the CRAY. Nevertheless, this quantum
Monte Carlo code is clearly a good example, in that parallel computers
easily (i.e., at same programming level) outperform the conventional
supercomputers.