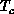 . As T approaches
. As T approaches 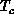 , the correlation length
, the correlation length
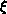 diverges as a power law with critical exponent
diverges as a power law with critical exponent  :
:





The Ising model is the simplest model for
ferromagnetism that predicts phase transitions
and critical phenomena. The spins are discrete and have only two
possible states. This model, introduced by Lenz in 1920
[Lenz:20a], was solved in one dimension by Ising in 1925
[Ising:25a], and in two dimensions by Onsager in 1944
[Onsager:44a]. However, it has not been solved analytically in
three dimensions, so Monte Carlo computer simulation methods have been
one of the methods used to obtain numerical solutions. One of the best
available techniques for this is the Monte Carlo Renormalization
Group (MCRG) method
[Wilson:80a], [Swendsen:79a]. The Ising model exhibits a
second-order phase transition in d=3 dimensions at a critical
temperature 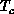 . As T approaches
. As T approaches 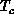 , the correlation length
, the correlation length
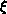 diverges as a power law with critical exponent
diverges as a power law with critical exponent  :
:
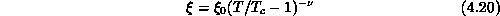
and the
pair correlation function 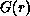 at
at 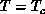 falls off to zero with
distance r as a power law defining the critical
exponent
falls off to zero with
distance r as a power law defining the critical
exponent 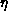 :
:
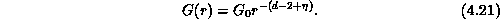
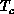 ,
,  and
and 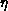 determine
the critical behavior of the 3-D Ising model and it is their values we
wish to determine using MCRG.
determine
the critical behavior of the 3-D Ising model and it is their values we
wish to determine using MCRG.
In 1984, this was done by Pawley, Swendsen, Wallace and Wilson
[Pawley:84a] in Edinburgh on the ICL DAP computer with high statistics.
They ran on four lattice sizes-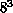 ,
, 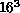 ,
, 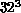 and
and 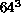 -measuring
seven even and six odd spin operators. We are essentially repeating their
calculation on the new AMT DAP computer. Why should we do this? First, to
investigate finite size effects-we have run on the biggest lattice used by
Edinburgh,
-measuring
seven even and six odd spin operators. We are essentially repeating their
calculation on the new AMT DAP computer. Why should we do this? First, to
investigate finite size effects-we have run on the biggest lattice used by
Edinburgh, 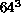 , and on a bigger one,
, and on a bigger one, 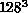 . Second, to investigate
truncation effects-qualitatively the more operators we measure for MCRG,
the better, so we have included 53 even and 46 odd operators. Third, we are
making use of the new cluster-updating algorithm due to Swendsen and Wang
[Swendsen:87a], implemented according to Wolff [Wolff:89b].
Fourth, we would like to try to measure another critical exponent more
accurately-the correction-to-scaling exponent
. Second, to investigate
truncation effects-qualitatively the more operators we measure for MCRG,
the better, so we have included 53 even and 46 odd operators. Third, we are
making use of the new cluster-updating algorithm due to Swendsen and Wang
[Swendsen:87a], implemented according to Wolff [Wolff:89b].
Fourth, we would like to try to measure another critical exponent more
accurately-the correction-to-scaling exponent  , which plays an
important role in the analysis.
, which plays an
important role in the analysis.
The idea behind MCRG is that the correlation length diverges at the critical point, so that certain quantities should be invariant under ``renormalization'', which here means a transformation of the length scale. On the lattice, we can double the lattice size by, for example, ``blocking'' the spin values on a square plaquette into a single spin value on a lattice with 1/4 the number of sites. For the Ising model, the blocked spin value is given the value taken by the majority of the 4 plaquette spins, with a random tie-breaker for the case where there are 2 spins in either state. Since quantities are only invariant under this MCRG procedure at the critical point, this provides a method for finding the critical point.
In order to calculate the quantities of interest using MCRG, one must
evaluate the spin operators 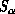 . In [Pawley:84a], the
calculation was restricted to seven even spin operators and six odd; we
evaluated 53 and 46, respectively [Baillie:91d]. Specifically, we decided
to evaluate the most important operators in a
. In [Pawley:84a], the
calculation was restricted to seven even spin operators and six odd; we
evaluated 53 and 46, respectively [Baillie:91d]. Specifically, we decided
to evaluate the most important operators in a 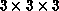 cube
[Baillie:88h]. To determine the critical coupling (or inverse
temperature),
cube
[Baillie:88h]. To determine the critical coupling (or inverse
temperature), 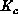 , one performs independent Monte Carlo simulations
on a large lattice L of size
, one performs independent Monte Carlo simulations
on a large lattice L of size 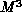 and on smaller lattices S of
size
and on smaller lattices S of
size 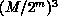 ,
, 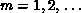 , and compares the operators
measured on the large lattice blocked m times more than the smaller
lattices.
, and compares the operators
measured on the large lattice blocked m times more than the smaller
lattices. 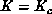 when they are the same. Since the effective
lattice sizes are the same, unknown finite size effects should cancel.
The critical exponents,
when they are the same. Since the effective
lattice sizes are the same, unknown finite size effects should cancel.
The critical exponents, 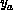 , are obtained directly from the
eigenvalues,
, are obtained directly from the
eigenvalues, 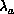 , of the
stability matrix,
, of the
stability matrix, 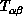 , which measures changes between
different blocking levels, according to
, which measures changes between
different blocking levels, according to 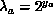 . In particular, the leading eigenvalue
. In particular, the leading eigenvalue 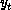 of
of
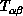 for the even
for the even 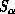 gives
gives  from
from 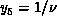 , and, similarly,
, and, similarly, 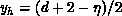 from the odd eigenvalue
from the odd eigenvalue
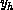 of
of 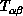 .
.
The Distributed Array Processor (DAP) is a SIMD computer consisting of
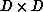 bit-serial processing elements (PEs) configured as a
cyclic two-dimensional grid with nearest-neighbor connectivity. The
Ising model computer simulation is well suited to such a machine since
the spins can be represented as single-bit (logical) variables. In
three-dimensions, the system of spins is configured as an
bit-serial processing elements (PEs) configured as a
cyclic two-dimensional grid with nearest-neighbor connectivity. The
Ising model computer simulation is well suited to such a machine since
the spins can be represented as single-bit (logical) variables. In
three-dimensions, the system of spins is configured as an 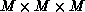 simple cubic lattice, which is ``crinkle mapped'' onto the
simple cubic lattice, which is ``crinkle mapped'' onto the 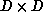 DAP by storing
DAP by storing 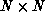 pieces of each of M planes in each PE:
pieces of each of M planes in each PE:
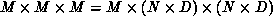 , with
, with
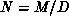 . Our Monte Carlo simulation uses a hybrid algorithm in which
each sweep consists of 10 standard Metropolis
[Metropolis:53a] spin updates followed by one cluster update using
Wolff's single-cluster variant of the Swendsen and Wang algorithm. On
the
. Our Monte Carlo simulation uses a hybrid algorithm in which
each sweep consists of 10 standard Metropolis
[Metropolis:53a] spin updates followed by one cluster update using
Wolff's single-cluster variant of the Swendsen and Wang algorithm. On
the 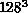 lattice, the autocorrelation time of the magnetization
reduces from
lattice, the autocorrelation time of the magnetization
reduces from 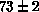 sets of 100 sweeps for Metropolis alone to
sets of 100 sweeps for Metropolis alone to
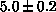 sets of 10 Metropolis plus one cluster update for the
hybrid algorithm. In order to measure the spin operators,
sets of 10 Metropolis plus one cluster update for the
hybrid algorithm. In order to measure the spin operators, 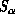 ,
the DAP code simply histograms the spin configurations so that an
analysis program can later pick out each particular spin operator using
a look-up table. Currently, the code requires the same time to do one
histogram measurement, one Wolff single-cluster update or 100
Metropolis updates. Therefore, our hybrid of 10 Metropolis plus one
cluster update takes about the same time as a measurement. On a
DAP 510, this hybrid update takes on average 127 secs (13.5 secs) for
the
,
the DAP code simply histograms the spin configurations so that an
analysis program can later pick out each particular spin operator using
a look-up table. Currently, the code requires the same time to do one
histogram measurement, one Wolff single-cluster update or 100
Metropolis updates. Therefore, our hybrid of 10 Metropolis plus one
cluster update takes about the same time as a measurement. On a
DAP 510, this hybrid update takes on average 127 secs (13.5 secs) for
the 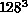 (
(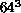 ) lattices. We have performed simulations on
) lattices. We have performed simulations on 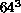 and
and 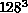 lattices at two values of the coupling:
lattices at two values of the coupling: 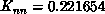 (Edinburgh's best estimate of the critical coupling) and
(Edinburgh's best estimate of the critical coupling) and
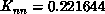 . We accumulated
. We accumulated 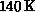 measurements for each
of the
measurements for each
of the 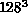 simulations and
simulations and 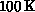 for the
for the 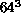 so that the
total time used for this calculation is roughly 11,000 hours. For
error analysis, this is divided into bins of
so that the
total time used for this calculation is roughly 11,000 hours. For
error analysis, this is divided into bins of 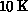 measurements.
measurements.
In analyzing our results, the first thing we have to decide is the
order in which to arrange our 53 even and 46 odd spin operators.
Naively, they can be arranged in order of increasing total distance
between the spins [Baillie:88h] (as was done in
[Pawley:84a]). However, the ranking of a spin operator is
determined physically by how much it contributes to the energy of the
system. Thus, we did our analysis initially with the operators in the
naive order to calculate their energies, then subsequently we used the
``physical'' order dictated by these energies. This physical order of
the first 20 even operators is shown in Figure 4.12 with
6 of Edinburgh's operators indicated; the 7th Edinburgh operator
(E-6) is our 21st. This order is important in assessing the systematic
effects of truncation, as we are going to analyze our data as a
function of the number of operators included. Specifically, we
successively diagonalize the 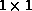 ,
, 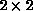 ,
,  ,
(
,
(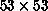 for even,
for even, 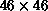 for odd) stability matrix
for odd) stability matrix
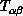 to obtain its eigenvalues and, thus, the critical
exponents.
to obtain its eigenvalues and, thus, the critical
exponents.
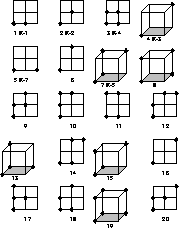
Figure 4.12: Our Order for Even Spin Operators
We present our results in terms of the eigenvalues of the even and odd
parts of 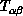 . The leading even eigenvalue on the first
four blocking levels starting from the
. The leading even eigenvalue on the first
four blocking levels starting from the 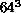 lattice
is plotted against the number of operators included in the analysis in
Figure 4.13, and on the first five blocking
levels starting from the
lattice
is plotted against the number of operators included in the analysis in
Figure 4.13, and on the first five blocking
levels starting from the 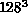 lattice in Figure 4.14.
Similarly, the leading odd eigenvalues for
lattice in Figure 4.14.
Similarly, the leading odd eigenvalues for 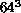 and
and 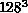 lattices
are shown in Figures 4.15 and 4.16,
respectively. First of all, note that there are significant truncation
effects-the value of the eigenvalues do not settle down until at
least 30 and perhaps 40 operators are included. We note also
that our value agrees with Edinburgh's when around 7 operators are
included-this is a significant verification that the two calculations
are consistent. With most or all of the operators included, our values
on the two different lattice sizes agree, and the agreement improves
with increasing blocking levels. Thus, we feel that we
have overcome the finite size effects so that a
lattices
are shown in Figures 4.15 and 4.16,
respectively. First of all, note that there are significant truncation
effects-the value of the eigenvalues do not settle down until at
least 30 and perhaps 40 operators are included. We note also
that our value agrees with Edinburgh's when around 7 operators are
included-this is a significant verification that the two calculations
are consistent. With most or all of the operators included, our values
on the two different lattice sizes agree, and the agreement improves
with increasing blocking levels. Thus, we feel that we
have overcome the finite size effects so that a 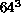 lattice is just
large enough. However, the advantage in going to
lattice is just
large enough. However, the advantage in going to 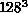 is obvious in
Figures 4.14 and 4.16: There, we can
perform one more blocking , which reveals that the
results on the fourth and fifth blocking levels are
consistent. This means that we have eliminated most of the transient
effects near the fixed point in the MCRG procedure. We also see that
the main limitation of our calculation is statistics-the error bars
are still rather large for the highest blocking level.
is obvious in
Figures 4.14 and 4.16: There, we can
perform one more blocking , which reveals that the
results on the fourth and fifth blocking levels are
consistent. This means that we have eliminated most of the transient
effects near the fixed point in the MCRG procedure. We also see that
the main limitation of our calculation is statistics-the error bars
are still rather large for the highest blocking level.
Now in order to obtain values for  and
and 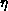 , we must extrapolate
our results from a finite number of blocking levels to
an infinite number. This is done by fitting the corresponding
eigenvalues
, we must extrapolate
our results from a finite number of blocking levels to
an infinite number. This is done by fitting the corresponding
eigenvalues 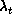 and
and 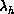 according to
according to
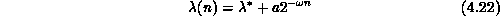
where 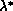 is the extrapolated value and
is the extrapolated value and  is the
correction-to-scaling exponent. Therefore, we first need to calculate
is the
correction-to-scaling exponent. Therefore, we first need to calculate
 , which comes directly from the second leading even
eigenvalue:
, which comes directly from the second leading even
eigenvalue: 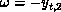 . Our best estimate is in the interval
. Our best estimate is in the interval
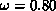 -0.85, and we use the value 0.85 for the purpose of
extrapolation, since it gives the best fits. The final results are
-0.85, and we use the value 0.85 for the purpose of
extrapolation, since it gives the best fits. The final results are
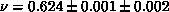 ,
, 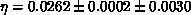 ,
where the first errors are statistical and the second errors are
estimates of the systematic error coming from the uncertainty in
,
where the first errors are statistical and the second errors are
estimates of the systematic error coming from the uncertainty in
 .
.
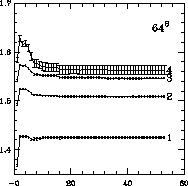
Figure 4.13: Leading Even Eigenvalue on  Lattice
Lattice
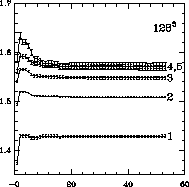
Figure 4.14: Leading Even Eigenvalue on  Lattice
Lattice
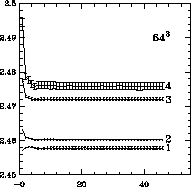
Figure 4.15: Leading Odd Eigenvalue on  Lattice
Lattice
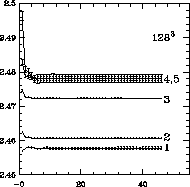
Figure 4.16: Leading Odd Eigenvalue on  Lattice
Lattice
Finally, perhaps the most important number, because it can be
determined the most accurately, is 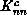 . By comparing the fifth
blocking level on the
. By comparing the fifth
blocking level on the 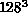 lattice to the fourth on
the
lattice to the fourth on
the 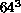 lattice for both coupling values and taking a weighted mean,
we obtain
lattice for both coupling values and taking a weighted mean,
we obtain 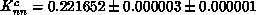 , where again
the first error is statistical and the second is systematic.
, where again
the first error is statistical and the second is systematic.
Thus, MCRG calculations give us very accurate values for the three
critical parameters 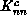 ,
, 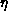 , and
, and  , and give a
reasonable estimate for
, and give a
reasonable estimate for  . Each parameter is obtained
independently and directly from the data. We have shown that
truncation and finite-size errors at all but the highest
blocking level have been reduced to below the
statistical errors. Future high statistics simulations on
. Each parameter is obtained
independently and directly from the data. We have shown that
truncation and finite-size errors at all but the highest
blocking level have been reduced to below the
statistical errors. Future high statistics simulations on 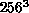 lattices will significantly reduce the remaining errors and allow us to
determine the exponents very accurately.
lattices will significantly reduce the remaining errors and allow us to
determine the exponents very accurately.




