Analysis of Alpha-Beta Pruning

The standard source on mathematical analysis of the alpha-beta algorithm is the paper by Knuth and Moore [Knuth:75a]. This paper gives a complete analysis for perfectly ordered trees, and derives some results about randomly ordered trees. We will concern ourselves here with perfectly ordered trees, since real chess programs achieve almost-perfect ordering.

  
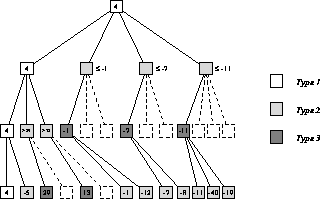
Figure: Pruning of a Perfectly Ordered Tree. The tree of Figures 14.3 and 14.4 has been extended another ply, and also the move ordering has been rearranged so that the best move is always searched first. By classifying the nodes into types as described in the text, the following pattern emerges: All children of type one and three nodes are searched, while only the first child of a type two node is searched.

In this context, perfect move-ordering means that in any position, we always consider the best move first. Ordering of the rest of the moves does not matter. Knuth and Moore show that in a perfectly ordered tree, the nodes can be divided into three types, as illustrated by Figure 14.7. As in previous figures, nodes are assumed to be generated and searched in left-to-right order. The typing of the nodes is as follows. Type one nodes are on the ``principal variation.'' The first child of a type one node is type one and the rest of the children are type two. Children of type two nodes are type three, and children of type three nodes are type two.

How much parallelism is available at each node? The pruning of the perfectly ordered tree of Figure 14.7 offers a clue. By thinking through the alpha-beta procedure, one notices the following pattern:

• All children of type one nodes are searched,
• Only the first child of a type two node is searched-the rest are pruned; and
• All children of type three nodes must be searched.

The implications of this for a parallel search are important. To efficiently search a perfectly ordered tree in parallel, one should perform the following algorithm.

• At type one nodes, the first child must be searched sequentially (in order to initialize the alpha-beta bounds), then the rest can be searched in parallel.
• At type two nodes, there is no parallelism since only one child will be searched (time spent searching other children will be wasted).
• Type three nodes, on the other hand, are fully parallel and all the children can be searched independently and simultaneously.

The key for parallel search of perfectly ordered chess trees, then, is to stay sequential at type two nodes, and go parallel at type three nodes. In the non-perfectly ordered case, the clean distinction between node types breaks down, but is still approximately correct. In our program, the hash table plays a role in deciding upon the node type. The following strategy is used by a master processor when reaching a node of the chess tree:

Make an inquiry to the hash table regarding this position. If the hash table suggests a move, search it first, sequentially. In this context, ``sequentially'' means that the master takes her slaves with her down this line of play. This is to allow possible parallelism lower down in the tree. If no move is suggested or the suggested move fails to cause an alpha-beta cutoff, search the remaining moves in parallel. That is, farm the work out to the slaves in a self-scheduled manner.