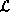 , the dynamics of the
fields
, the dynamics of the
fields 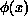 are determined through the action functional
are determined through the action functional





In order to explain the computations for QCD, we use the Feynman path
integral formalism [Feynman:65a]. For any
field theory described by a Lagrangian density 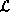 , the dynamics of the
fields
, the dynamics of the
fields 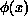 are determined through the action functional
are determined through the action functional
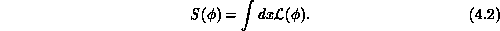
In this language, the measurement of a physical observable represented by an
operator  is given as the expectation value
is given as the expectation value
where the partition function Z is
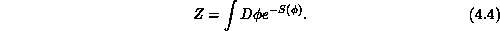
In these expressions, the integral  indicates a sum over all possible
configurations of the field
indicates a sum over all possible
configurations of the field 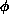 . A typical observable would be a product
of fields
. A typical observable would be a product
of fields 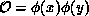 , which says how the fluctuations in the
field are correlated, and in turn, tells us something about the particles
that can propagate from point x to point y. The appropriate correlation
functions give us, for example, the masses of the various particles in the
theory. Thus, to evaluate almost any quantity in field theories like QCD,
one must simply evaluate the corresponding path integral. The catch is that
the integrals range are over an infinite-dimensional space.
, which says how the fluctuations in the
field are correlated, and in turn, tells us something about the particles
that can propagate from point x to point y. The appropriate correlation
functions give us, for example, the masses of the various particles in the
theory. Thus, to evaluate almost any quantity in field theories like QCD,
one must simply evaluate the corresponding path integral. The catch is that
the integrals range are over an infinite-dimensional space.
To put the field theory onto a computer, we begin by discretizing space and
time into a lattice of points. Then the functional
integral is simply defined as the product of the
integrals over the fields at every site of the lattice 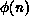 :
:
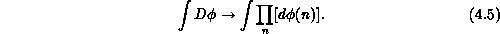
Restricting space and time to a finite box, we end up with a finite (but
very large) number of ordinary integrals, something we might imagine doing
directly on a computer. However, the high dimensionality of these
integrals renders conventional mesh techniques impractical. Fortunately, the
presence of the exponential 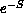 means that the integrand is sharply
peaked in one region of configuration space. Hence, we resort to a
statistical treatment and use Monte Carlo type algorithms to sample the
important parts of the integration region [Binder:86a].
means that the integrand is sharply
peaked in one region of configuration space. Hence, we resort to a
statistical treatment and use Monte Carlo type algorithms to sample the
important parts of the integration region [Binder:86a].
Monte Carlo algorithms typically begin with some initial
configuration of fields, and then make pseudorandom changes on the fields
such that the ultimate probability P of generating a particular field
configuration 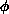 is proportional to the Boltzmann factor,
is proportional to the Boltzmann factor,
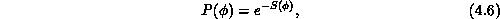
where 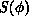 is the action associated with the given configuration.
There are several ways to implement such a scheme, but for many theories the
simple Metropolis algorithm [Metropolis:53a]
is effective. In this algorithm, a new configuration
is the action associated with the given configuration.
There are several ways to implement such a scheme, but for many theories the
simple Metropolis algorithm [Metropolis:53a]
is effective. In this algorithm, a new configuration 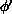 is generated by
updating a single variable in the old configuration
is generated by
updating a single variable in the old configuration 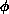 and calculating
the change in action (or energy)
and calculating
the change in action (or energy)
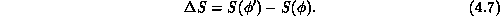
If 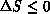 , the change is accepted; if
, the change is accepted; if 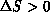 , the change
is accepted with probability
, the change
is accepted with probability 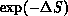 . In practice, this is done
by generating a pseudorandom number r in the
interval [0,1] with uniform probability distribution, and accepting the
change if
. In practice, this is done
by generating a pseudorandom number r in the
interval [0,1] with uniform probability distribution, and accepting the
change if 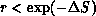 . This is guaranteed to generate the
correct (Boltzmann) distribution of configurations, provided ``detailed
balance'' is satisfied. That condition means
that the probability of proposing the change
. This is guaranteed to generate the
correct (Boltzmann) distribution of configurations, provided ``detailed
balance'' is satisfied. That condition means
that the probability of proposing the change 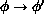 is
the same as that of proposing the reverse process
is
the same as that of proposing the reverse process
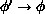 . In practice, this is true if we never
simultaneously update two fields which interact directly via the
action. Note that this constraint has important ramifications for
parallel computers as we shall see below.
. In practice, this is true if we never
simultaneously update two fields which interact directly via the
action. Note that this constraint has important ramifications for
parallel computers as we shall see below.
Whichever method one chooses to generate field configurations, one updates
the fields for some equilibration time of E steps, and then calculates the
expectation value of 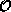 in Equation 4.3 from the next T
configurations as
in Equation 4.3 from the next T
configurations as
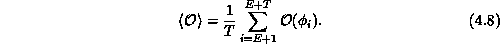
The statistical error in Monte Carlo behaves as 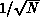 , where N is
the number of statistically independent configurations.
, where N is
the number of statistically independent configurations. 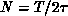 , where
, where
 is known as the autocorrelation time. This autocorrelation time can
easily be large, and most of the computer time is spent in generating effectively
independent configurations. The operator measurements then become a small
overhead on the whole calculation.
is known as the autocorrelation time. This autocorrelation time can
easily be large, and most of the computer time is spent in generating effectively
independent configurations. The operator measurements then become a small
overhead on the whole calculation.




