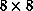 (i.e., n = 8), and let the number of (virtual) processors be p = 4.
The following is a possible sequence of actions that the programmer could do
using the tool.
(i.e., n = 8), and let the number of (virtual) processors be p = 4.
The following is a possible sequence of actions that the programmer could do
using the tool.





For the sake of illustration, let the size of A and B be 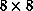 (i.e., n = 8), and let the number of (virtual) processors be p = 4.
The following is a possible sequence of actions that the programmer could do
using the tool.
(i.e., n = 8), and let the number of (virtual) processors be p = 4.
The following is a possible sequence of actions that the programmer could do
using the tool.
After examining the data dependences within the program segment as reported
by the tool, let us assume that the programmer decides to partition A
by column and B by row. The tool computes the internal mapping:\
A$(1) = A(1:8, 1:2) and B$(1) = B(1:2, 1:8).
A$(2) = A(1:8, 3:4) and B$(2) = B(3:4, 1:8).
A$(3) = A(1:8, 5:6) and B$(3) = B(5:6, 1:8).
A$(4) = A(1:8, 7:8) and B$(4) = B(7:8, 1:8).
To determine the communication necessary, the tool uses Algorithm COMM, shown in Figure 13.8. For simple partitioning schemes as found in many applications, the communication computed by algorithm COMM can be parameterized by processor number, that is, evaluated once for an arbitrary processor. In addition, we are also investigating other methods to speed up the algorithm.

Figure 13.8: Algorithm to Determine the Communication Induced by the Data
Partitioning Scheme
Consider program P1 for example. According to algorithm COMM, when the
kth processor executes the first statement, the required communication is
given by
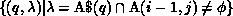
where the range of i and j are determined by the section of the LHS
owned by processor k, in this case 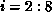 and
and 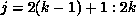 (since A
is partitioned columnwise). But the partitioning of A ensures that
(since A
is partitioned columnwise). But the partitioning of A ensures that
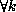 , the data
, the data 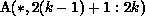 is always local to
k. The set of
is always local to
k. The set of 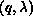 pairs will, therefore, be an empty set for
any k. Thus, the execution of the first statement with A partitioned by
column requires no communication.
pairs will, therefore, be an empty set for
any k. Thus, the execution of the first statement with A partitioned by
column requires no communication.
When the kth processor executes the second statement, the communication as computed by algorithm COMM is given by
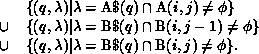
The ranges of i and j are determined by the section of the LHS that is
owned by processor k: in this case 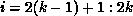 and
and 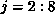 (since B
is partitioned rowwise). The second and third terms will be
(since B
is partitioned rowwise). The second and third terms will be  ,
because the row partitioning of B ensures that
,
because the row partitioning of B ensures that 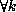 , the data
, the data
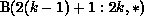 is always local to k. The first term can be
a nonempty set, because processor k owns a column of A (i.e., j in
the range
is always local to k. The first term can be
a nonempty set, because processor k owns a column of A (i.e., j in
the range 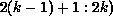 ), while the range of j in the first term is
), while the range of j in the first term is 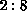 .
Thus, communication may be required to get the nonlocal element of A before
the kth processor can proceed with the computation of its
.
Thus, communication may be required to get the nonlocal element of A before
the kth processor can proceed with the computation of its 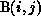 .
The dependence from the definition of
.
The dependence from the definition of 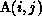 to its use is
loop-independent. Algorithm COMM therefore computes commlevel, the
common nesting level of the source and sink of the dependence, to be the
level of the inner i loop. The section
to its use is
loop-independent. Algorithm COMM therefore computes commlevel, the
common nesting level of the source and sink of the dependence, to be the
level of the inner i loop. The section 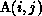 translated to the
level of the inner i loop is simply the single element
translated to the
level of the inner i loop is simply the single element 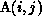 .
Thus, each message communicates this single element and the communication
occurs within the inner i loop.
.
Thus, each message communicates this single element and the communication
occurs within the inner i loop.
The execution of program P1 results in a large number of messages because each message only communicates a single element of A, and the communication occurs within the inner loop. Message startup and transmission costs are specified by the target machine parameters, and the average cost of each message is determined from the performance model. The tool computes the communication cost by multiplying the number of messages by the average cost of sending a single element message. This cost estimate is returned to the programmer.
Now consider the program P2, with the same partitioning scheme for A and B. When the kth processor executes the first statement, the required communication as determined by algorithm COMM is given by
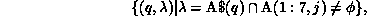
where the range of j is determined by the section of the LHS
owned by processor k, in this case 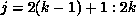 (since A is
partitioned columnwise). Note that in this case,
(since A is
partitioned columnwise). Note that in this case, 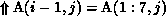 . This is because commlevel is now the level of the
outer j loop, so that the section
. This is because commlevel is now the level of the
outer j loop, so that the section 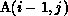 must be translated to
the level of the j loop. In other words, the reference to
must be translated to
the level of the j loop. In other words, the reference to 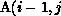 )
in the first statement results in an access of the first seven elements of
the jth column of A, during each iteration of the j loop. Since A is
partitioned columnwise, this section will always be available locally in
each processor, so that the above set is empty and no communication is
required.
)
in the first statement results in an access of the first seven elements of
the jth column of A, during each iteration of the j loop. Since A is
partitioned columnwise, this section will always be available locally in
each processor, so that the above set is empty and no communication is
required.
When processor k executes the second statement, the communication required is given by
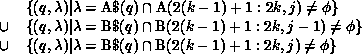
The second and third terms will be empty sets since the required part of B is
local to each k (because B is partitioned rowwise). The first term will
be nonempty, because each processor owns 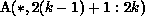 , and
the range of j in the first term is outside the range
, and
the range of j in the first term is outside the range 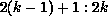 . The
data required by processor k from processor q will therefore be a strip
. The
data required by processor k from processor q will therefore be a strip
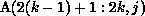 , from each
, from each 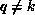 .
.
This data can be communicated between the two inner do i loops. Each
message will communicate a 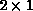 size strip of A. Fewer exchanges will
be required compared to program P1, because each exchange now communicates a
strip of A, and the communication occurs outside the inner loop. Once again,
the performance model and target machine parameters are used by the tool to
estimate the total communication cost, and this cost is returned to the
programmer.
size strip of A. Fewer exchanges will
be required compared to program P1, because each exchange now communicates a
strip of A, and the communication occurs outside the inner loop. Once again,
the performance model and target machine parameters are used by the tool to
estimate the total communication cost, and this cost is returned to the
programmer.
For most target machines, the communication cost in program P2 will be considerably less than in program P1, because of larger message size and fewer messages.
Next, let us consider program P3. Assuming that the same partitioning scheme is used for A and B, the execution of the first loop by the kth processor will require communication given by
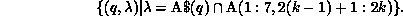
But this is an empty set because of the column partitioning of A. Here
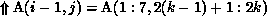 , because commlevel
for this case is the level of the subroutine that contains the two loops.
The section is, therefore, translated to this level by substituting the
appropriate bounds for i and j. The translated section indicates that the
reference
, because commlevel
for this case is the level of the subroutine that contains the two loops.
The section is, therefore, translated to this level by substituting the
appropriate bounds for i and j. The translated section indicates that the
reference 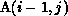 in the first statement results in an access of the
section
in the first statement results in an access of the
section 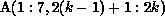 during all iterations of the outer
j loop that are executed by processor k.
during all iterations of the outer
j loop that are executed by processor k.
When the kth virtual processor executes the second loop, the required communication is
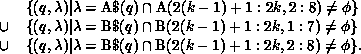
The second and third terms will be empty sets because of the row
partitioning of B. The first term will be nonempty, and the data required by
processor k from processor q will be the block 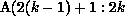 ,
,
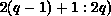 , for each
, for each 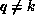 . This block can be communicated between
the two do j loops.
. This block can be communicated between
the two do j loops.
This communication can be done between the two loops, allowing computation
within each of the two loops to proceed in parallel. The number of messages
is the fewest for this case because a 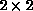 block of A is communicated
during each exchange. Program P3 is thus likely to give superior performance
compared to P1 or P2, on most machines. We ran programs P1, P2 and P3 with
A partitioned by column and B by row, on 16 processors of the nCUBE at
Caltech. The functions
block of A is communicated
during each exchange. Program P3 is thus likely to give superior performance
compared to P1 or P2, on most machines. We ran programs P1, P2 and P3 with
A partitioned by column and B by row, on 16 processors of the nCUBE at
Caltech. The functions 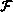 and
and 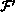 consisted of one and two
double-precision floating-point operations, respectively. The results of the
experiment are shown in Figure 13.9. The graphs clearly illustrate
the performance improvement that occurs due to reduction in number of
messages and increase in length of each message.
consisted of one and two
double-precision floating-point operations, respectively. The results of the
experiment are shown in Figure 13.9. The graphs clearly illustrate
the performance improvement that occurs due to reduction in number of
messages and increase in length of each message.
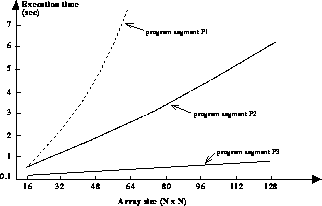
Figure 13.9: Timing Results for Programs P1, P2 and P3 on the nCUBE, Using 16
Processors.




