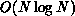Mesh-based algorithms have started to incorporate adaptive mesh refinement to decrease storage and wasted computational effort. Instead of solving the entire system with a fixed resolution grid designed to represent the finest structures, local regions may be refined adaptively depending on accuracy requirements such as the density of particles. Unlike finite-element and finite-volume algorithms, which deform a single grid by shifting or adding vertices, adaptive mesh refinement (AMR) algorithms simply overlay regions of interest with increasingly fine rectangular meshes. Berger, Colella, and Oliger have pioneered application of this method to hyperbolic partial differential equations [Berger:84a;89a]. Almgren recently has extended AMR for multigrid to an MLC implementation [Almgren:91a].
Adaptive mesh refinement traditionally has been limited to rectangular regions. McCormick and Quinlan have extended their very robust, inherently conservative adaptive mesh multilevel algorithm called asynchronous fast adaptive composite (AFAC) [McCormick:89a] to relax nonrectangular subregions directly between two grid levels. The algorithm is a true multiscale solver not limited to relaxation-type solvers. AFAC provides special benefits for parallel implementations because the various levels in a single multigrid cycle may be scheduled in any convenient order and combined at the end of the cycle instead of the traditional, sequentially-ordered V-cycle.
In the particle-based solver regime, the Barnes-Hut [Barnes:86a] method
utilizes an adaptive tree to store information about one particle or the
collective information about particles in the subcubes. Each particle
calculates the force on itself from all of the other particles in the
simulation by querying the hierarchical database, descending each branch of
the tree until a user-specified accuracy criterion has been met. The
accuracy is determined by the solid angle subtended by the cluster of
particles within the cube from the vantage point of the particle
calculating the force. If the cube contains a single particle or if all of
the particles in the cube can be approximated by the center of mass, the
force is computed using a multipole expansion; otherwise, each of the eight
subcubes is examined in turn using the same criterion. By utilizing
combined information instead of the individual data at the terminal node of
each branch, the algorithm requires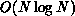 
operations.
Section 12.4 provides additional explanation while describing a
parallel implementation of this method.
The Fast Multipole Method(FMM) developed by
Greengard and Rokhlin [Greengard:87b] utilizes new techniques to
quickly compute and combine the multipole approximations in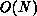 
operations. Initial implementations sorted the particles into groups
on a fixed level of the tree with the hierarchical pyramid structure
providing the communication network used to combine and repropagate the
multipole-calculated potential. Recent enhancements include adaptive
refinement of the hierarchy-creating structures similar to a Barnes-Hut
tree [Greengard:91a].
Both Katzenelson and Anderson have noted the applicability of a variety of ``tree algorithms'' to the N-body problem. Katzenelson utilizes the common structure of the Barnes-Hut and FMM algorithms to study how this problem can be mapped to a variety of parallel computer designs [Katzenelson:89a]. Anderson utilizes the multigrid framework as a basis for communication in his FMM implementation which substitutes Poisson integrals for spherical harmonic multipole expansions [Anderson:90b].