




Next: 12.7.3 Shellsort or Diminishing
Up: 12.7 Sorting
Previous: 12.7.1 The Merge Strategy
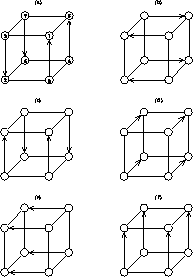
Figure 12.29: Bitonic Scheme for d=3. This figure illustrates the six
compare-exchange steps of the bitonic algorithm for
d=3. Each diagram illustrates four compare-exchange processes which happen
simultaneously. The arrows represent a compare-exchange between
two processors. The largest items go to the processor at the point of
the arrow, and the smallest items to the one at the base of the arrow.
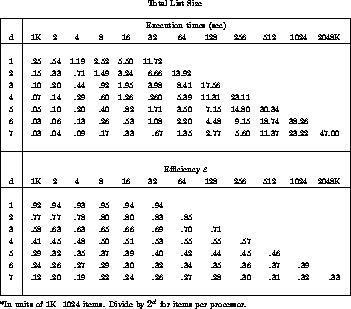
Table 12.2: Bitonic sort on a hypercube. The rows are labelled by
hypercube size ( ), the columns by number of items
to sort.
), the columns by number of items
to sort.
Many algorithms for sorting on concurrent machines are based upon Batcher's
bitonic sorting algorithm ([Batcher:68a],
[Knuth:73a, pp.232-3]). The first step in the merge
strategy is for each processor to internally sort via quicksort. One
is then left with the problem of constructing a series of
compare-exchange steps which will correctly merge 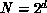 sorted
sublists. This problem is completely isomorphic to the problem of
sorting a list of
sorted
sublists. This problem is completely isomorphic to the problem of
sorting a list of  items by pairwise comparisons between items.
Each one of our sublist compare-exchange operations is equivalent to a
single compare-exchange between two individual items. The pattern of
compare-exchanges for the bitonic algorithm for the d=3 case is shown
in Figure 12.29. More details and a specification of the
bitonic algorithm can be found in Chapter 18 of [Fox:88a].
items by pairwise comparisons between items.
Each one of our sublist compare-exchange operations is equivalent to a
single compare-exchange between two individual items. The pattern of
compare-exchanges for the bitonic algorithm for the d=3 case is shown
in Figure 12.29. More details and a specification of the
bitonic algorithm can be found in Chapter 18 of [Fox:88a].
Table 12.2 shows the actual times and efficiencies for our
implementation of the bitonic algorithm. Results are shown for sorting lists
of sizes 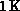 to
to 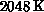 items on hypercubes with dimensions,
d, ranging from one (2 nodes) to seven (128 nodes). Efficiencies are
computed by comparing with single-processor times to quicksort the entire
list (we take quicksort to be our benchmark sequential algorithm). The same
information is also shown graphically in Figure 12.30.
items on hypercubes with dimensions,
d, ranging from one (2 nodes) to seven (128 nodes). Efficiencies are
computed by comparing with single-processor times to quicksort the entire
list (we take quicksort to be our benchmark sequential algorithm). The same
information is also shown graphically in Figure 12.30.
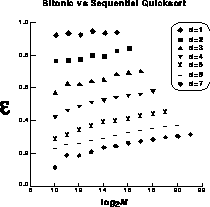
Figure 12.30: The Efficiency of the Bitonic Algorithm Versus
List Size for Various Size Hypercubes-Labelled by Cube Dimension d.
Clearly, the efficiencies fall off rapidly with increasing d. From the
standpoint of cost-effectiveness, this algorithm is a failure. On the other
hand, Table 12.2 shows that for fixed-list sizes and increasing
machine size, the execution times continue to decrease. So, from the
speed-at-any-cost point of view, the algorithm is a success. We attribute the
inefficiency of the bitonic algorithm partly to communication overhead and
some load imbalance during the compare-exchanges, but mostly to
nonoptimality of the algorithm itself. In our definition of efficiency we
are comparing the parallel bitonic algorithm to sequential quicksort. In
bitonic, the number of cycles grows quadratically with d. This suggests
that efficiency can be improved greatly by using a parallel algorithm that
sorts in fewer operations without sacrificing concurrency.





Next: 12.7.3 Shellsort or Diminishing
Up: 12.7 Sorting
Previous: 12.7.1 The Merge Strategy
Guy Robinson
Wed Mar 1 10:19:35 EST 1995







 ), the columns by number of items
to sort.
), the columns by number of items
to sort.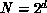 sorted
sublists. This problem is completely isomorphic to the problem of
sorting a list of
sorted
sublists. This problem is completely isomorphic to the problem of
sorting a list of  items by pairwise comparisons between items.
Each one of our sublist compare-exchange operations is equivalent to a
single compare-exchange between two individual items. The pattern of
compare-exchanges for the bitonic algorithm for the d=3 case is shown
in Figure
items by pairwise comparisons between items.
Each one of our sublist compare-exchange operations is equivalent to a
single compare-exchange between two individual items. The pattern of
compare-exchanges for the bitonic algorithm for the d=3 case is shown
in Figure 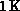 to
to 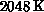 items on hypercubes with dimensions,
d, ranging from one (2 nodes) to seven (128 nodes). Efficiencies are
computed by comparing with single-processor times to quicksort the entire
list (we take quicksort to be our benchmark sequential algorithm). The same
information is also shown graphically in Figure
items on hypercubes with dimensions,
d, ranging from one (2 nodes) to seven (128 nodes). Efficiencies are
computed by comparing with single-processor times to quicksort the entire
list (we take quicksort to be our benchmark sequential algorithm). The same
information is also shown graphically in Figure 