Vortex methods (see [Leonard:80a]) are used to simulate incompressible flows at high Reynolds number. The two-dimensional inviscid vorticity equation,
is solved by discretizing the vorticity field into Lagrangian vortex particles,
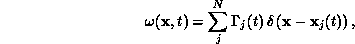
where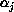 
is the strength or the circulation of the 
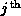particle. For an incompressible flow, the knowledge of the vorticity is
sufficient to reconstruct the velocity field. Using complex notation, the
induced velocity is given by
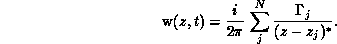
The velocity is evaluated at each particle location and the discrete Lagrangian elements are simply advected at the local fluid velocity. In this way, the numerical scheme approximately satisfies Kelvin and Helmholtz theorems that govern the motion of vortex lines. The numerical approximations have transformed the original partial differential equation into a set of 2N ordinary differential equations, an N-body problem. This class of problems is encountered in many fields of computational physics, for example, molecular dynamics, gravitational interactions, plasma physics and, of course, vortex dynamics.