




Next: Optimization Methods
for
Up: 9.8 Munkres Algorithm for
Previous: 9.8.2 The Sequential Algorithm
The timing results from Figure 9.20 clearly dictate the manner
in which the calculations in Munkres algorithm should be distributed among
the nodes of a hypercube for concurrent execution. The zero and minimum
element searches for Steps 3 and 5 are the most time consuming and should
be done concurrently. In contrast, the essentially bookkeeping tasks
associated with Steps 2 and 4 require insignificant CPU time and are most
naturally done in lockstep (i.e., all nodes of the hypercube perform the same
calculations on the same data at the same time). The details of the
concurrent algorithm are as follows.
Data Decomposition
The distance matrix 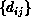 is distributed across the
nodes of the hypercube, with entire columns assigned to individual
nodes. (This assumes, effectively, that
is distributed across the
nodes of the hypercube, with entire columns assigned to individual
nodes. (This assumes, effectively, that 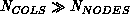 ,
which is always the case for assignment problems which are big enough
to be ``interesting.'') The cover and zero locator lists defined in
Section 9.8.2 are duplicated on all nodes.
,
which is always the case for assignment problems which are big enough
to be ``interesting.'') The cover and zero locator lists defined in
Section 9.8.2 are duplicated on all nodes.
Task Decomposition
The concurrent implementation of Step 5 is particularly
trivial. Each node first finds its own minimum uncovered value,
setting this value to some ``infinite'' token if all columns assigned
to the node are covered. A simple loop on communication channels
determines the global minimum among the node-by-node minimum values,
and each node then modifies the contents of its local portion of the
distance matrix according to Steps 5.2 and 5.3.
The concurrent implementation of Step 3 is just slightly more awkward. On
entry to Step 3, each node searches for zeros according to the rules of
Section 9.8.2, and fills a three-element status list:
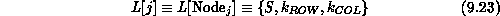
where S is a zero-search status flag,
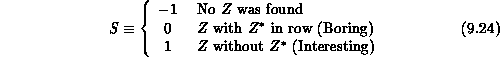
If the status is nonnegative, the last two entries in the status list
specify the location of the found zero. A simple channel loop is used to
collect the individual status lists of each node into all nodes, and the
action taken next by the program is as follows:
- If all nodes give negative status (no Z found), all nodes proceed
to Step 5.
- If any node gives status one, all nodes proceed to Step 4 for lockstep
updates of the zero location lists, using the row-column indices of the node
which gave status one as the starting point for Step 4.1. If more than one
node returns status one (highly unlikely, in practice), only the first such
node (lower node number) is used.
- If all zeros uncovered are ``Boring,'' the cover switching in Step 3.3
of the algorithm is performed. This is done in lockstep, processing the Zs
returned by the nodes in order of increasing node number. Note that the cover
rearrangements performed for one node may well cover a Z returned by a node
with a higher node number. In such cases, the nominal Z returned by the
later node is simply ignored.
It is worth emphasizing that only the actual searches for zero and
minimum entries in Steps 3 and 5 are done concurrently. The updates of
the cover and zero locator lists are done in unison.
The concurrent algorithm has been implemented on the Mark III hypercube, and
has been tested against random point association tasks for a variety of list
sizes. Before examining results of these tests, however, it is worth noting
that the concurrent implementation is not particularly dependent on the
hypercube topology. The only communication-dependent parts of the algorithm
are
- Determination of the ensemble-wide minimum value for Step 5;
- Collection of the local Step 3 status lists
(Equation 9.24),
either of which could be easily done for almost any MIMD architecture.
Table 9.7 presents performance results for the association of
random lists of 200 points on the Mark III hypercube for various cube
dimensions. (For consistency, of course, the same input lists are used for
all runs.) Time values are given in CPU seconds for the total execution
time, as well as the time spent in Steps 3 and 5. Also given are the
standard concurrent execution efficiencies,
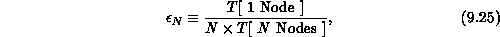
as well as the number of times the Step 3 box of Figure 9.19
is entered during execution of the algorithm. The numbers of entries into
the other boxes of Figure 9.19 are independent of the hypercube
dimension.
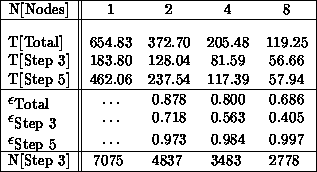
Table 9.7: Concurrent Performance for 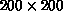 Random Points. T
is time,
Random Points. T
is time,  efficiency, and N[Step 3] the number of times
Step 3 is executed.
efficiency, and N[Step 3] the number of times
Step 3 is executed.
There is an aspect of the timing results in Table 9.7 which
should be noted. Namely, essentially all inefficiencies of the
concurrent algorithm are associated with Step 3 for two nodes compared to
Step 3 for one node. The times spent in Step 5 are approximately halved for
each increase in the dimension of the hypercube. However, the efficiencies
associated with the zero searching in Step 3 are rather poorer, particularly
for larger numbers of nodes.
At a simple, qualitative level, the inefficiencies associated with Step 3 are
readily understood. Consider the task of finding a single zero located
somewhere inside an 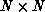 matrix. The mean sequential search time is
matrix. The mean sequential search time is

since, on average, half of the entries of the matrix will be examined before
the zero is found. Now consider the same zero search on two nodes. The node
which has the half of the matrix containing the zero will find it in about
half the time of Equation 9.26. However, the other node
will always search through all of its 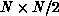 items before
returning a null status for Equation 9.24. Since the node
which found the zero must wait for the other node before the (lockstep)
modifications of zero locators and cover tags, the node without the zero
determines the actual time spent in Step 3, so that
items before
returning a null status for Equation 9.24. Since the node
which found the zero must wait for the other node before the (lockstep)
modifications of zero locators and cover tags, the node without the zero
determines the actual time spent in Step 3, so that
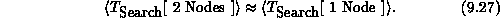
In the full program, the concurrent bottleneck is not as bad as
Equation 9.27 would imply. As noted above, the concurrent
algorithm can process multiple ``Boring'' Zs in a single pass through Step 3.
The frequency of such multiple Zs per step can be estimated by noting the
decreasing number of times Step 3 is entered with increasing hypercube
dimension, as indicated in Table 9.7. Moreover, each node
maintains a counter of the last column searched during Step 3. On subsequent
re-entries, columns prior to this marked column are searched for zeros only
if they have had their cover tag changed during the prior Step 3 processing.
While each of these algorithm elements does diminish the problems associated
with Equation 9.27, the fact remains that the search for zero
entries in the distributed distance matrix is the least efficient step in
concurrent implementations of Munkres algorithm.
The results presented in Table 9.7 demonstrate that an
efficient implementation of Munkres algorithm is certainly feasible.
Next, we examine how these efficiencies change as the problem size
is varied.
The results shown in Tables 9.8 and 9.9
demonstrate an improvement of concurrent efficiencies with increasing problem
size-the expected result. For the 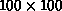 problem on eight nodes,
the efficiency is only about 50%. This problem is too small for eight
nodes, with only 12 or 13 columns of the distance matrix assigned to
individual nodes.
problem on eight nodes,
the efficiency is only about 50%. This problem is too small for eight
nodes, with only 12 or 13 columns of the distance matrix assigned to
individual nodes.
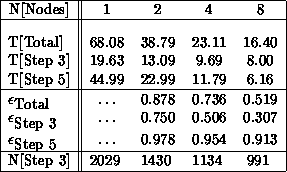
Table 9.8: Concurrent Performance for 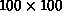 Random Points
Random Points
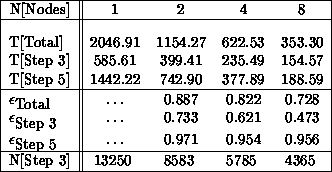
Table 9.9: Concurrent Performance for 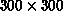 Random Points
Random Points
While the performance results in Tables 9.7 through
9.9 are certainly acceptable, it is nonetheless
interesting to investigate possible improvements of efficiency for the
zero searches in Step 3. The obvious candidate for an algorithm
modification is some sort of checkpointing: At intermediate times
during the zero search, the nodes exchange a ``Zero Found Yet?'' status
flag, with all nodes breaking out of the zero search loop if any node
returns a positive result.
For message-passing machines such as the Mark III, the checkpointing scheme is
of little value, as the time spent in individual entries to Step 3 is not
enormous compared to the node-to-node communication time. For example, for
the two-node solution of the 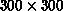 problem, the mean time for a
single entry to Step 3 is only about
problem, the mean time for a
single entry to Step 3 is only about  , compared to a typical
node-to-node communications time which can be a significant fraction of a
millisecond. The time required to perform a single Step 3 calculation is not
large compared to node-to-node communications. As a (not unexpected)
consequence, all attempts to improve the Step 3 efficiencies through various
``Found Anything?'' schemes were completely unsuccessful.
, compared to a typical
node-to-node communications time which can be a significant fraction of a
millisecond. The time required to perform a single Step 3 calculation is not
large compared to node-to-node communications. As a (not unexpected)
consequence, all attempts to improve the Step 3 efficiencies through various
``Found Anything?'' schemes were completely unsuccessful.
The checkpointing difficulties for a message-passing machine could disappear,
of course, on a shared-memory machine. If the zero-search status flags for
the various nodes could be kept in memory locations readily (i.e., rapidly)
accessible to all nodes, the problems of the preceding paragraph might be
eliminated. It would be interesting to determine whether significant
improvements on the (already good) efficiencies of the concurrent Munkres
algorithm could be achieved on a shared-memory machine.





Next: Optimization Methods
for
Up: 9.8 Munkres Algorithm for
Previous: 9.8.2 The Sequential Algorithm
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
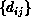 is distributed across the
nodes of the hypercube, with entire columns assigned to individual
nodes. (This assumes, effectively, that
is distributed across the
nodes of the hypercube, with entire columns assigned to individual
nodes. (This assumes, effectively, that 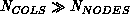 ,
which is always the case for assignment problems which are big enough
to be ``interesting.'') The cover and zero locator lists defined in
Section 9.8.2 are duplicated on all nodes.
,
which is always the case for assignment problems which are big enough
to be ``interesting.'') The cover and zero locator lists defined in
Section 9.8.2 are duplicated on all nodes.





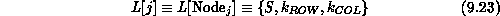
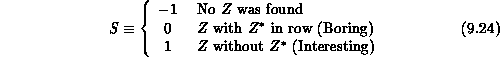
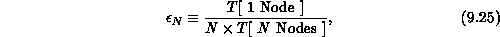

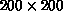 Random Points. T
is time,
Random Points. T
is time,  efficiency, and N[Step 3] the number of times
Step 3 is executed.
efficiency, and N[Step 3] the number of times
Step 3 is executed.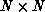 matrix. The mean sequential search time is
matrix. The mean sequential search time is

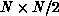 items before
returning a null status for Equation
items before
returning a null status for Equation 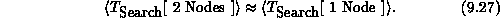
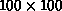 problem on eight nodes,
the efficiency is only about 50%. This problem is too small for eight
nodes, with only 12 or 13 columns of the distance matrix assigned to
individual nodes.
problem on eight nodes,
the efficiency is only about 50%. This problem is too small for eight
nodes, with only 12 or 13 columns of the distance matrix assigned to
individual nodes.

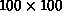 Random Points
Random Points
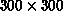 Random Points
Random Points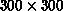 problem, the mean time for a
single entry to Step 3 is only about
problem, the mean time for a
single entry to Step 3 is only about  , compared to a typical
node-to-node communications time which can be a significant fraction of a
millisecond. The time required to perform a single Step 3 calculation is not
large compared to node-to-node communications. As a (not unexpected)
consequence, all attempts to improve the Step 3 efficiencies through various
``Found Anything?'' schemes were completely unsuccessful.
, compared to a typical
node-to-node communications time which can be a significant fraction of a
millisecond. The time required to perform a single Step 3 calculation is not
large compared to node-to-node communications. As a (not unexpected)
consequence, all attempts to improve the Step 3 efficiencies through various
``Found Anything?'' schemes were completely unsuccessful.