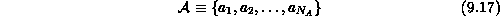
The so-called assignment problem is of considerable importance in a variety of applications, and can be stated as follows. Let
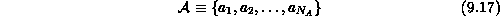
and
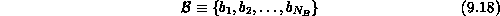
be two sets of items, and let
be a measure of the distance (dissimilarity) between individual items from
the two lists. Taking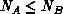 
, the objective of the assignment
problem is to find the particular mapping
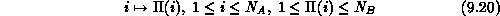
such that the total association score
is minimized over all permutations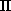 
.
For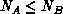 
, the naive (exhaustive search) complexity of the
assignment problem is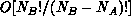 
. There are,
however, a variety of exact solutions to the assignment problem with reduced
complexity 
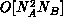([Blackman:86a], [Burgeios:71a],
[Kuhn:55a]). Section 9.8.2 briefly describes one such method,
Munkres algorithm [Kuhn:55a], and presents a
particular sequential
implementation. Performance of the algorithm is examined for the
particularly nasty problem of associating lists of random points within the
unit square. In Section 9.8.3, the algorithm is generalized for
concurrent execution, and performance results for runs on the Mark III
hypercube are presented.
