Next, we turn to Equation 9.11's (that is, IVP's) concurrent numerical solution via the DASSL algorithm. We cover the major computational steps in abstract, and we also describe the generic aspects of proto-Cdyn in this connection. In the subsequent section, we discuss issues peculiar to the distillation simulation.
Broadly, the concurrent solution of IVP consists of three block operations: startup, dynamic simulation, and a cleanup phase. Significant concurrency is apparent only in the dynamic simulation phase. We will assume that the simulation interval requested generates enough work so that the startup and cleanup phases prove insignificant by comparison and consequently pose no serious Amdahl's-law bottleneck. Given this assumption, we can restrict our attention to a single step of IVP as illustrated schematically in Figure 9.15.
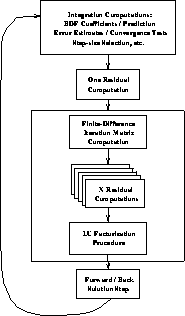
Figure 9.15: Major Computational Blocks of a Single Integration Step.A single step in the integration begins with a number of BDF-related
computations, including the solution ``prediction'' step. Then,
``correction'' is achieved through Newton iteration steps, each involving a
Jacobian computation, and linear-system solution (LU factorization plus
forward- and back-solves). The computation of the Jacobian in turn relies upon
multiple independent residual calculations, as shown. The three items
enclosed in the rounded rectangle (Jacobian computation-through at most N
Residual computations-and LU factorization) are, in practice, computed less
often than the others-the old Jacobian matrix is used in the iteration loop
until convergence slows intolerably.
In the startup phase, a sequential host program interprets the user specification for the simulation. From this it generates the concurrent database: the templates and their mutual interconnections, data needed by particular templates, and a distribution of this information among the processes that are to participate. The processes are themselves spawned and fed their respective databases. Once they receive their input information, the processes rebuild the data structures for interfacing with Concurrent DASSL, and for generating the residuals. Tolerances and initial derivatives must be computed and/or estimated. Furthermore, in each process column, the processes must rendezvous to finalize their communication labelling for the transmission of states and nonstates to be performed during the residual calculation. This provides the basis for a reactive, deadlock-free update procedure described below.
The cleanup phase basically retrieves appropriate state values and returns them to the host for propagation to the user. Cleanup may be interspersed intermittently with the actual dynamic simulation. It provides a simple record of the results of simulation and terminates the concurrent processes at the simulation's conclusion.
The dynamic simulation phase consists of repetitive prediction and correction steps, and marches in time. Each successful time step requires the solution of one or more instances of Equation 9.12-additional time steps that converge but fail to satisfy error tolerances, or fail to converge quickly enough, are necessarily discarded. In the next section, we cover aspects of these operations in more detail, for a single step.