The topic of this section is the implementation and concurrent performance of sparse, unsymmetric LU factorization for medium-grain multicomputers. Our target hardware is distributed-memory, message-passing concurrent computers such as the Symult s2010 and Intel iPSC/2 systems. For both of these systems, efficient cut-through wormhole routing technology provides pairwise communication performance essentially independent of the spatial location of the computers in the ensemble [Athas:88a]. The Symult s2010 is a two-dimensional, mesh-connected concurrent computer; all examples in this paper were run on this variety of hardware. Message-passing performance, portability, and related issues relevant to this work are detailed in [Skjellum:90a].
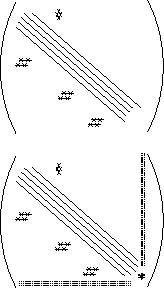
Figure 9.11: An Example of Jacobian Matrix Structures. In
chemical-engineering process flowsheets, Jacobians with main-band
structure, lower-triangular structure (feedforwards), upper-triangular
structure (feedbacks), and borders (global or artificially restructured
feedforwards and/or feedbacks) are common.
Questions of linear-algebra performance are pervasive throughout scientific and engineering computation. The need for high-quality, high-performance linear algebra algorithms (and libraries) for multicomputer systems therefore requires no attempt at justification. The motivation for the work described here has a specific origin, however. Our main higher level research goal is the concurrent dynamic simulation of systems modelled by ordinary differential and algebraic equations; specifically, dynamic flowsheet simulation of chemical plants (e.g., coupled distillation columns) [Skjellum:90c]. Efficient sequential integration algorithms solve staticized nonlinear equations at each time point via modified Newton iteration (cf., [Brenan:89a], Chapter 5). Consequently, a sequence of structurally identical linear systems must be solved; the matrices are finite-difference approximations to Jacobians of the staticized system of ordinary differential-algebraic equations. These Jacobians are large, sparse, and unsymmetric for our application area. In general, they possess both band and significant off-band structure. Generic structures are depicted in Figure 9.11. This work should also bear relevance to electric power network/grid dynamic simulation where sparse, unsymmetric Jacobians arise, and elsewhere.