




Next: 8.3.5 Selected Results
Up: 8.3.4 Performance
Previous: Mark IIIfp
Performance of the original port of the parallel code from the
Mark IIIfp to a 64-processor iPSC/860 hypercube, while adequate, was
below expectations based on the 4:1 ratio of 64-bit floating-point peak
speeds. Moreover, initial runs on up to 512 nodes of the
Delta indicated very poor speedups. Timings at
the subroutine level revealed that an excessive amount of time was
being spent both in matrix multiplication and in construction of the
distributed transformation matrix. Optimization is still in progress,
and performance is still a small fraction of the machine's peak speed,
but some improvements have been made.
Several steps were taken to improve the matrix multiplication.
Blocking sends and receives were replaced with asynchronous NX
routines, overlapping communication with computation; the absolute
number of communications was reduced by grouping together small data
blocks and by computing rather than communicating block sizes; one of
the matrices was transposed in order to maximize the length of the
innermost loop; and finally, the inner loop was replaced with a
level-one BLAS call. Presently the
floating-point work proceeds at 7 to 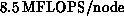 , including
loop overhead, depending on problem size. On the iPSC/860, throughput
for the subroutine as a whole is generally limited by communication
bandwidth to approximately
, including
loop overhead, depending on problem size. On the iPSC/860, throughput
for the subroutine as a whole is generally limited by communication
bandwidth to approximately 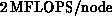 . We
expect to increase this by better matching the sizes of the two
matrices being multiplied, which will require minor modifications in
the top-level routine. Higher throughput, approximately
. We
expect to increase this by better matching the sizes of the two
matrices being multiplied, which will require minor modifications in
the top-level routine. Higher throughput, approximately 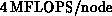 , is obtained on the Delta. Further improvement is
certainly possible, but communication overhead on the Delta is already
below 10% for the application as a whole, and matrix multiplication
time is no longer a major limitation.
, is obtained on the Delta. Further improvement is
certainly possible, but communication overhead on the Delta is already
below 10% for the application as a whole, and matrix multiplication
time is no longer a major limitation.
Reducing the time spent in constructing the transformation matrix proved to
be a matter of removing index computations in the innermost loops. In the
original implementation, integer modulo arithmetic was used on each call to
determine the local components of the transformation matrix. This form of
parallel overhead proved surprisingly costly. It was essentially eliminated
by precomputing and storing three lists of pointers to the data elements
needed locally. These pointers are used for indirect indexing of elements
needed in a vector-vector outer product, which now runs at approximately
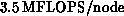 . (Preceding the outer product with an explicit
gather using the same pointers was tested, but proved counterproductive.)
A BLAS call (daxpy), timed at 13.1 to
. (Preceding the outer product with an explicit
gather using the same pointers was tested, but proved counterproductive.)
A BLAS call (daxpy), timed at 13.1 to
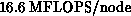 for typical cases, was inserted elsewhere.
Construction of the transformation matrices is now typically 1% of the
total time, with throughput, including all logic and integer arithmetic
as overhead, around
for typical cases, was inserted elsewhere.
Construction of the transformation matrices is now typically 1% of the
total time, with throughput, including all logic and integer arithmetic
as overhead, around 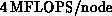 .
.
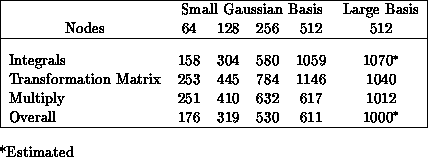
Table 8.6: SMC Performance on the Delta (MFLOPS)
In the present state of the program, the perfectly parallel
integral-calculation step is the dominant element in most of our
calculations, as desired and expected based on the amount of
floating-point work. It is also the most complex step, however, with
little linear algebra but with many math library calls (sin, cos, exp,
sqrt), floating-point divides, and branches. Not surprisingly,
therefore, it is comparatively slow. We have timed the CRAY version at
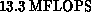 on a single-processor Y-MP, reflecting the routine's
intrinsically scalar character. Present performance on the i860 is
about
on a single-processor Y-MP, reflecting the routine's
intrinsically scalar character. Present performance on the i860 is
about 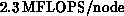 . Some additional optimization is planned,
but substantial improvement may have to await more mature versions of
the compiler and libraries.
. Some additional optimization is planned,
but substantial improvement may have to await more mature versions of
the compiler and libraries.
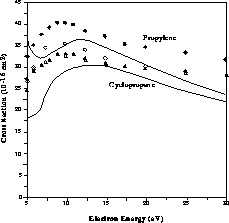
Figure 8.10: Calculated Integral Elastic Cross Sections for Electron Scattering
by the C H
H Isomers Cyclopropane and Propylene. For comparison,
experimental total cross sections of Refs. [Floeder:85a] (open symbols) and
[Nishimura:91a] (filled symbols) are shown; triangles are cyclopropane and
circles propylene data.
Isomers Cyclopropane and Propylene. For comparison,
experimental total cross sections of Refs. [Floeder:85a] (open symbols) and
[Nishimura:91a] (filled symbols) are shown; triangles are cyclopropane and
circles propylene data.
With the program components as described above, the present code should
run on 512 nodes of the Delta at a sustained rate of approximately 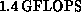 . In practice, lower performance is obtained, due to
synchronization delays, load imbalance, file I/O, etc.
Actual timings taken from 64- to 512-node production runs are given in
Table 8.6. The limited data available for the
integral-evaluation package reflects the difficulty of obtaining an
accurate operation count; for the case shown, a count was obtained
using flow-tracing utilities on a CRAY. For the ``large'' case shown
in the table, we estimate overall performance at
. In practice, lower performance is obtained, due to
synchronization delays, load imbalance, file I/O, etc.
Actual timings taken from 64- to 512-node production runs are given in
Table 8.6. The limited data available for the
integral-evaluation package reflects the difficulty of obtaining an
accurate operation count; for the case shown, a count was obtained
using flow-tracing utilities on a CRAY. For the ``large'' case shown
in the table, we estimate overall performance at 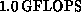 ,
inclusive of all I/O and overhead, on 512 nodes of the Delta; this
estimate is based on an approximate operation count for the integral
package and actual counts for the remaining routines.
,
inclusive of all I/O and overhead, on 512 nodes of the Delta; this
estimate is based on an approximate operation count for the integral
package and actual counts for the remaining routines.





Next: 8.3.5 Selected Results
Up: 8.3.4 Performance
Previous: Mark IIIfp
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
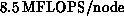 , including
loop overhead, depending on problem size. On the iPSC/860, throughput
for the subroutine as a whole is generally limited by communication
bandwidth to approximately
, including
loop overhead, depending on problem size. On the iPSC/860, throughput
for the subroutine as a whole is generally limited by communication
bandwidth to approximately 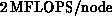 . We
expect to increase this by better matching the sizes of the two
matrices being multiplied, which will require minor modifications in
the top-level routine. Higher throughput, approximately
. We
expect to increase this by better matching the sizes of the two
matrices being multiplied, which will require minor modifications in
the top-level routine. Higher throughput, approximately 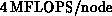 , is obtained on the Delta. Further improvement is
certainly possible, but communication overhead on the Delta is already
below 10% for the application as a whole, and matrix multiplication
time is no longer a major limitation.
, is obtained on the Delta. Further improvement is
certainly possible, but communication overhead on the Delta is already
below 10% for the application as a whole, and matrix multiplication
time is no longer a major limitation.





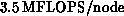 . (Preceding the outer product with an explicit
gather using the same pointers was tested, but proved counterproductive.)
A BLAS
. (Preceding the outer product with an explicit
gather using the same pointers was tested, but proved counterproductive.)
A BLAS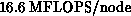 for typical cases, was inserted elsewhere.
Construction of the transformation matrices is now typically 1% of the
total time, with throughput, including all logic and integer arithmetic
as overhead, around
for typical cases, was inserted elsewhere.
Construction of the transformation matrices is now typically 1% of the
total time, with throughput, including all logic and integer arithmetic
as overhead, around 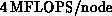 .
.

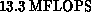 on a single-processor Y-MP, reflecting the routine's
intrinsically scalar character. Present performance on the i860 is
about
on a single-processor Y-MP, reflecting the routine's
intrinsically scalar character. Present performance on the i860 is
about 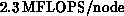 . Some additional optimization is planned,
but substantial improvement may have to await more mature versions of
the compiler and libraries.
. Some additional optimization is planned,
but substantial improvement may have to await more mature versions of
the compiler and libraries.

 H
H Isomers Cyclopropane and Propylene. For comparison,
experimental total cross sections of Refs. [Floeder:85a] (open symbols) and
[Nishimura:91a] (filled symbols) are shown; triangles are cyclopropane and
circles propylene data.
Isomers Cyclopropane and Propylene. For comparison,
experimental total cross sections of Refs. [Floeder:85a] (open symbols) and
[Nishimura:91a] (filled symbols) are shown; triangles are cyclopropane and
circles propylene data.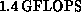 . In practice, lower performance is obtained, due to
synchronization delays, load imbalance, file I/O,
. In practice, lower performance is obtained, due to
synchronization delays, load imbalance, file I/O,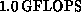 ,
inclusive of all I/O and overhead, on 512 nodes of the Delta; this
estimate is based on an approximate operation count for the integral
package and actual counts for the remaining routines.
,
inclusive of all I/O and overhead, on 512 nodes of the Delta; this
estimate is based on an approximate operation count for the integral
package and actual counts for the remaining routines.