




Next: 8.1.9 Conclusions
Up: 8.1 Full and Banded
Previous: 8.1.7 Concurrent Linear Algebra
The basic matrix algorithms appear to fall in the synchronous class in
the language of Section 3.4. Correspondingly, one would
expect to get good performance on SIMD machines. This is indeed true
for matrix multiplication, but it is hard to get good SIMD performance
on LU factorization and the more complicated matrix algorithms. Here
the algorithm is not fully synchronous. In particular, there are
several operations involving row or column operations. These lead to
two problems. Firstly, the parallelism is reduced from
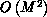 (for an
(for an 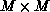 matrix) to
matrix) to 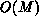 -this is
typically a serious problem on SIMD machines, such as the CM-2 or
Maspar MP-1,2 which are fine grain and require ``massive
parallelism.'' Secondly, the use of pivoting
clearly introduces irregularity into the algorithm, which complicates
the SIMD implementation. For these reasons, most research on matrix
algorithms has concentrated on MIMD multicomputers, such as the
hypercube.
-this is
typically a serious problem on SIMD machines, such as the CM-2 or
Maspar MP-1,2 which are fine grain and require ``massive
parallelism.'' Secondly, the use of pivoting
clearly introduces irregularity into the algorithm, which complicates
the SIMD implementation. For these reasons, most research on matrix
algorithms has concentrated on MIMD multicomputers, such as the
hypercube.
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
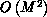 (for an
(for an 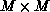 matrix) to
matrix) to 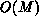 -this is
typically a serious problem on SIMD machines, such as the CM-2 or
Maspar MP-1,2 which are fine grain and require ``massive
parallelism.'' Secondly, the use of pivoting
clearly introduces irregularity into the algorithm, which complicates
the SIMD implementation. For these reasons, most research on matrix
algorithms has concentrated on MIMD multicomputers, such as the
hypercube.
-this is
typically a serious problem on SIMD machines, such as the CM-2 or
Maspar MP-1,2 which are fine grain and require ``massive
parallelism.'' Secondly, the use of pivoting
clearly introduces irregularity into the algorithm, which complicates
the SIMD implementation. For these reasons, most research on matrix
algorithms has concentrated on MIMD multicomputers, such as the
hypercube.




