Since matrix algorithms play such an important role in scientific computing, it is desirable to develop a library of linear algebra routines for concurrent multiprocessors. Ideally, these routines should be optimal and general-purpose, that is, portable to a wide variety of multiprocessors. Unfortunately, these two objectives are antagonistic, and an algorithm that is optimal on one machine will often not be optimal on another machine. Even among hypercubes it is apparent that the optimal decomposition, and hence the optimal algorithm, depends on the message latency, with a block decomposition being best for low latency machines, and a row decomposition often being best for machines with high latency. Another factor to be considered is that often a matrix algorithm is only part of a larger application code. Thus, the data decomposition before and after the matrix computation may not be optimal for the matrix algorithm itself. We are faced with the choice of either transforming the decomposition before and after the matrix computation so that the optimal matrix algorithm can be used, or leaving the decomposition as it is and using a suboptimal matrix algorithm. To summarize, the main issues that must be addressed are:
Two approaches to designing linear algebra libraries have been followed at Caltech. Fox, Furmanski, and Walker choose optimality as the most important concern in developing a set of linear algebra routines for low latency, homogeneous hypercubes, such as the Caltech/JPL Mark II hypercube. These routines feature the use of the scattered decomposition to ensure load balance, and to minimize communication costs. Transformations between decompositions are performed using the comutil library of global communication routines [Angus:90a], [Fox:88h], [Furmanski:88b]. This approach was mainly dictated by historical factors, rather than being a considered design decision-the hypercubes used most at Caltech up to 1987 were homogeneous and had low latency.
A different, and probably more useful approach, has been taken at Caltech by Van de Velde [Velde:89b] who opted for general-purpose library routines. The decomposition currently in use is passed to a routine through its argument list, so in general the decomposition is not changed and a suboptimal algorithm is used. The main advantage of this approach is that it is decomposition-independent and allows portability of code among a wide variety of multiprocessors. Also, the suboptimality of a routine must be weighed against the possibly large cost of transforming the data decomposition, so suboptimality does not necessarily result in a slower algorithm if the time to change the decomposition is taken into account.
Occasionally, it may be advantageous to change the decomposition, and most changes of this type are what Van de Velde calls orthogonal. In an orthogonal redistribution of the data, each pair of processors exchanges the same amount of data. Van de Velde has shown [Velde:90c] that any orthogonal redistribution can be performed by the following sequence of operations: Local permutation - Global transposition - Local permutation
A local permutation merely involves reindexing the local data within
individual processors. If we have P processors and P data items in each
processor, then the global transposition, 
, takes the item with local
index i in processor p and sends it to processor i, where it is stored
with local index p. Thus,
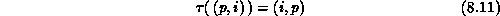
Van de Velde's transpose routine is actually a generalization of the hypercube-specific index routine in the comutil library.
Van de Velde has implemented his linear algebra library on the Intel iPSC/2 and the Symult 2010, and has used it in investigations of concurrent LU and QR factorization algorithms [Velde:89b], [Velde:90a], and in studies of invariant manifolds of dynamical systems [Lorenz:89a], [Velde:90b].
A group centered at Oak Ridge National Laboratory and the University of Tennessee is leading the development of a major new portable parallel full matrix library called ScaLAPACK [Choi:92a], [Choi:92b]. This is built around an elegant formulation of matrix problems in terms of the so-called level three BLAS, which are a set of submatrix operations introduced to support the basic LAPACK library [Anderson:90c], [Dongarra:90a]. This full matrix system embodies earlier ideas from LINPACK and EISPACK and is designed to ensure data locality and get good performance on shared-memory and vector supercomputers. The multicomputer ScaLAPACK is built around the scattered block decomposition described earlier.