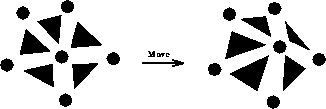Next: 7.2.4 Performance of String
Up: 7.2 Dynamically Triangulated Random
Previous: 7.2.2 Discretized Strings
In order to give the reader a feel for how one actually simulates a
dynamically triangulated random surface, we briefly explain our
computer program, string, which does this-more details can be
found in [Baillie:90e]. As we explained previously, in order to
incorporate the metric fluctuations, we randomly triangulate the
worldsheet of the string or random surface to obtain a mesh and make it
dynamical by allowing flips in the mesh that do not change the
topology. The incorporation of the flips into the simulation makes
vectorization difficult, so running on traditional supercomputers like
the Cray is not efficient. Similarly, the irregular nature of the
dynamically triangulated random surface inhibits efficient
implementation on SIMD computers like the Distributed Array Processor
and the Connection Machine. Thus, in order
to get a large amount of CPU power behind our random surface
simulations, we are forced to run on MIMD parallel computers.
Here, we have a choice of two main architectures: distributed-memory
hypercubes or shared-memory computers. We initially made use of the
former, as several machines of this type were available to us-all
running the same software environment, namely, ParaSoft's
Express System [ParaSoft:88a]. Having the same
software on different parallel computers makes porting the code from
one to another very easy. In fact, we ran our strings simulation
program on the nCUBE hypercube (for a total of 1800 hours on 512
processors), the Symult Series 2010 (900 hours on 64 processors), and
the Meiko Computing Surface (200 hours on 32 processors).
Since this simulation fits easily into the memory of a single node of
any of these hypercubes, we ran multiple simulations in
parallel-giving, of course, linear speedup. Each node was loaded
with a separate simulation (using a different random number generator seed), starting from a single mesh that has been
equilibrated elsewhere, say on a Sun workstation. After allowing a
suitable length of time for the meshes to decorrelate, data can be
collected from each node, treating them as separate experiments. More
recently, we have also run string on the GP1000 Butterfly (1000
hours on 14 processors) and TC2000 Butterfly II (500 hours on 14
processors) shared-memory computers-again with each processor
performing a unique simulation. Parallelism is thereby obtained by
``decomposing'' the space of Monte Carlo configurations.
The reason that we run multiple independent Monte Carlo simulations, rather than distribute the mesh over the
processors of the parallel computer, is that this domain decomposition
would be difficult for such an irregular problem. This is because,
with a distributed mesh, each processor wanting to change its part of
the mesh would have to first check that the affected pieces were not
simultaneously being changed by another processor. If they were,
detailed balance would be violated and the
Metropolis algorithm would no longer work. For a
regular lattice this is not a problem, since we can do a simple
red/black decomposition (Section 4.3); however this is not the
case for an irregular lattice. Similar parallelization difficulties
arise in other irregular Monte Carlo problems, such as gas and liquid
systems (Section 14.2). For the random surfaces application,
the size of the system which can be simulated using independent
parallelism is limited not by memory requirements, but by the time
needed to decorrelate the different meshes on each processor, which
grows rapidly with the number of nodes in the mesh.
The mesh is set up as a linked list in the
programming language C, using software developed at Caltech for doing
computational fluid dynamics on unstructured triangular meshes, called
DIME (Distributed Irregular Mesh Environment)
[Williams:88a;90b]
(Sections 10.1 and 10.2). The logical structure is that
of a set of triangular elements corresponding to the faces of the
triangulation of the worldsheet, connected via nodes corresponding to
the nodes of the triangulation of the worldsheet. The data required in
the simulation (of random surfaces or computational fluid
dynamics) is then stored in either
the nodes or the elements. We simulate a worldsheet with a fixed
number of nodes, N, which corresponds to the partition function of
Equation 7.1 evaluated at a fixed area. We also fix the
topology of the mesh to be spherical. (The results for other
topologies, such as a torus, are similar). The Monte Carlo procedure
sweeps through the mesh moving the Xs which live at the nodes, and
doing a Metropolis accept/reject. It then sweeps through the mesh a
second time doing the flips, and again performs a Metropolis
accept/reject at each attempt. Figure 7.5 illustrates
the local change to the mesh called a flip. For any edge, there
is a triangle on each side, forming the quadrilateral ABCD, and the
flip consists of changing the diagonal AC to BD. Both types of Monte
Carlo updates to the mesh can be implemented by identifying which
elements and nodes would be affected by the change, then
- saving the data from these affected elements
and nodes;
- making the proposed change;
- recalculating the element data;
- recalculating the node data;
- calculating the change in the action
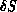 as the difference of
the sums of the new and the old action contributions from the affected nodes;
as the difference of
the sums of the new and the old action contributions from the affected nodes;
- given
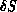 , deciding whether to accept or reject the change using
the standard Metropolis algorithm-if the change
is rejected, we replace the
element and node data with the saved values; if accepted, we need do nothing
since the change has already been made.
, deciding whether to accept or reject the change using
the standard Metropolis algorithm-if the change
is rejected, we replace the
element and node data with the saved values; if accepted, we need do nothing
since the change has already been made.

Figure 7.5: Flip Move
For the X move, the affected elements are the neighbors of node i, and
the affected nodes are the node i itself and its node neighbors, as shown
in Figure 7.6. For the flip, the affected elements are the
two sharing the edge, and the affected nodes are the four neighbor nodes of
these elements, as shown in Figure 7.7.
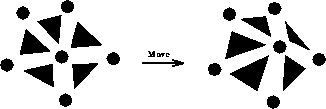
Figure 7.6: Nodes and Elements Affected by X Move

Figure 7.7: Nodes and Elements Affected by Flip Move





Next: 7.2.4 Performance of String
Up: 7.2 Dynamically Triangulated Random
Previous: 7.2.2 Discretized Strings
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
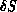 as the difference of
the sums of the new and the old action contributions from the affected nodes;
as the difference of
the sums of the new and the old action contributions from the affected nodes;
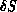 , deciding whether to accept or reject the change using
the standard Metropolis algorithm-if the change
is rejected, we replace the
element and node data with the saved values; if accepted, we need do nothing
since the change has already been made.
, deciding whether to accept or reject the change using
the standard Metropolis algorithm-if the change
is rejected, we replace the
element and node data with the saved values; if accepted, we need do nothing
since the change has already been made.