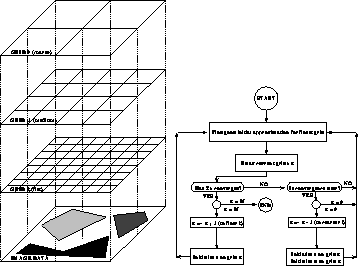
Figure 6.22: Pyramidal Structure for Multigrid Algorithms and General Flow of Control





The purpose of early vision is to undo the image formation process, recovering the properties of visible three-dimensional surfaces from the two-dimensional array of image intensities.
Computationally, this amounts to solving a very large system of equations. In general, the solution is not unique or does not exist (and therefore, one must settle for a suitable approximation).
The class of admissible solutions can be restricted by introducing a priori knowledge: the desired ``typical'' properties are enforced, transforming the inversion problem into the minimization of a functional. This is known as the regularization method [Poggio:85a]. Applying the calculus of variations, the stationary points are found by solving the Euler-Lagrange partial differential equations.
In standard methods for solving PDEs, the problem is first discretized on a finite-dimensional approximation space. The very large algebraic system obtained is then solved using, for example, ``relaxation'' algorithms which are local and iterative. The local structure is essential for the efficient use of parallel computation.
By the local nature of the relaxation process, solution errors on the scale of the solution grid step are corrected in a few iterations; however, larger scale errors are corrected very slowly. Intuitively, in order to correct them, information must be spread over a large scale by the ``sluggish'' neighbor-neighbor influence. If we want a larger spread of influence per iteration, we need large scale connections for the processing units, that is, we need to solve a simplified problem on a coarser grid.
The pyramidal structure of the multigrid solution grids is illustrated in Figure 6.22.

Figure 6.22: Pyramidal Structure for Multigrid Algorithms and General Flow of
Control
This simple idea and its realization in the multigrid algorithm
not only leads to asymptotically optimal solution times (i.e.,
convergence in 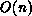 operations), but also
dramatically decreases solution times for a variety of practical
problems, as shown in [Brandt:77a].
operations), but also
dramatically decreases solution times for a variety of practical
problems, as shown in [Brandt:77a].
The multigrid ``recipe'' is very simple. First use relaxation to obtain an approximation with smooth error on a fine grid. Then, given the smoothness of the error, calculate corrections to this approximation on a coarser grid, and to do this first relax, then correct recursively on still coarser grids. Optionally, you can also use nested iteration (that coarser grids provide a good starting point for finer grids) to speed up the initial part of the computation.
Historically, these ideas were developed starting from the 1960s by Bakhvalov, Fedorenko, and others (see Stüben, et al. [Stuben:82a]). The sequential multigrid algorithm has been used for solving PDEs associated with different early vision problems in [Terzopoulos:86a].
It is shown in [Brandt:77a] that, with a few modifications in the basic algorithms, the actual solution (not the error) can be stored in each layer (full approximation storage algorithm). This method is particularly useful for visual reconstruction where we are interested not only in the finest scale result, but also in the multiscale representation developed as a byproduct of the solution process.




