A global tridiagonal matrix
A ,
represented as three vectors
(DL, D, DU), should be
distributed over a one-dimensional
process grid assuming a block-column
data distribution. We assume that
the coefficient tridiagonal matrix
A
is of size 
(
)
and is represented by the following.
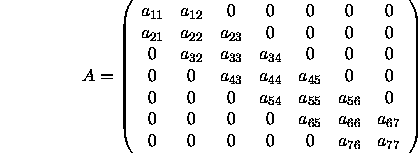
If we first assume that the matrix A is
nonsymmetric (diagonally dominant like),
and it is known a priori that no
pivoting is required for numerical stability,
the user may choose to perform no pivoting
during the factorization
(PxDTTRF ).
If we distribute this matrix
(assuming no pivoting) onto
a 
process grid
with a block size of 
,
the processes would contain the
local arrays found in figure 4.13.
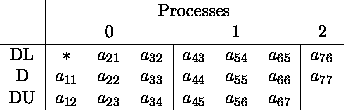
Figure 4.13: Mapping of local arrays for nonsymmetric tridiagonal
matrix A
Finally, a global symmetric positive definite tridiagonal matrix A , represented as two vectors (D and E), should be distributed over a one-dimensional process grid assuming a block-column data distribution.
Let us now assume that this matrix A
is symmetric positive definite and that
we distribute this matrix assuming lower
triangular storage (UPLO='L') onto a
process grid with a block
size . The processes would
contain the local arrays found in
figure 4.14. We would
then call the routine
PxPTTRF
to perform the factorization, for example.
Figure 4.14: Mapping of local arrays for symmetric positive definite
tridiagonal matrix A (UPLO='L')
If we then distributed this same
matrix assuming upper triangular
storage (UPLO='U') onto a
process grid with a block size ,
the processes would contain the local
arrays found in figure 4.15.
Figure 4.15: Mapping of local arrays for symmetric positive definite
tridiagonal matrix A (UPLO='U')
Note that in the tridiagonal cases,
it is not necessary to maintain the
empty storage positions as designated
by 
in the narrow band routines.
The matrix of right-hand-side vectors B (for example, used in PxDTTRS and PxPTTRS ) is assumed to be a dense matrix distributed block-row across the process grid. Thus, consecutive blocks of rows of the matrix B are assigned to successive processes in the process grid, as described in section 4.4.1.