This section is concerned with the solution of the generalized eigenvalue
problems 
, 
, and 
, where
A and B are real symmetric or complex Hermitian and B is positive definite.
Each of these problems can be reduced to a standard symmetric
eigenvalue problem, using a Cholesky factorization of B as either
or 
(
or 
in the Hermitian case).
With , we have
Hence the eigenvalues of are those of 
,
where C is the symmetric matrix 
and 
.
In the complex case C is Hermitian with 
and 
.
Table 3.11 summarizes how each of the three types of problem
may be reduced to standard form
, and how the eigenvectors z
of the original problem may be recovered from the eigenvectors y of the
reduced problem. The table applies to real problems; for complex problems,
transposed matrices must be replaced by conjugate transposes.
Table 3.11: Reduction of generalized symmetric definite eigenproblems to standard
problems
Given A and a Cholesky factorization of B,
the routines PxyyGST overwrite A
with the matrix C of the corresponding standard problem
(see table 3.12).
This may then be solved by using the routines described in
subsection 3.3.4.
No special routines are needed
to recover the eigenvectors z of the generalized problem from
the eigenvectors y of the standard problem, because these
computations are simple applications of Level 2 or Level 3 BLAS.
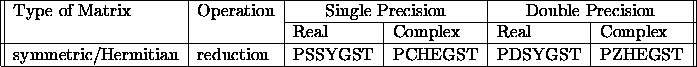
Table 3.12: Computational routines for the generalized symmetric definite eigenproblem