The singular value
decomposition (SVD) of a real m-by-n matrix A is defined as
follows. Let 
. The SVD of A is 
(
in the complex case), where
U and V are orthogonal (unitary) matrices and
is diagonal,
with 
.
The 
are the singular values of A and the leading
r columns 
of U and 
of V the
left and right singular vectors, respectively.
The SVD of a general matrix is computed by PxGESVD
(see subsection 3.2.3).
The approximate error
bounds
for the computed singular values
are
The approximate error bounds for the computed singular vectors
and 
,
which bound the acute angles between the computed singular vectors
and true singular vectors and , are
These bounds can be computing by the following code fragment:
EPSMCH = PSLAMCH( ICTXT, 'E' )
* Compute singular value decomposition of A
* The singular values are returned in S
* The left singular vectors are returned in U
* The transposed right singular vectors are returned in VT
CALL PSGESVD( 'V', 'V', M, N, A, IA, JA, DESCA, S, U, IU, JU,
$ DESCU, VT, IVT, JVT, DESCVT, WORK, LWORK, INFO )
IF( INFO.GT.0 ) THEN
PRINT *,'PSGESVD did not converge'
ELSE IF( MIN( M, N ).GT.0 ) THEN
SERRBD = EPSMCH * S( 1 )
* Compute reciprocal condition numbers for singular vectors
CALL SDISNA( 'Left', M, N, S, RCONDU, INFO )
CALL SDISNA( 'Right', M, N, S, RCONDV, INFO )
DO 10 I = 1, MIN( M, N )
VERRBD( I ) = EPSMCH*( S( 1 ) / RCONDV( I ) )
UERRBD( I ) = EPSMCH*( S( 1 ) / RCONDU( I ) )
10 CONTINUE
END IF
For example, if
and
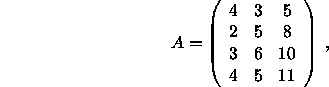
then the singular values, approximate error bounds, and true errors are given below.
