Error Bounds for the Symmetric Eigenproblem

 

The eigendecomposition  of an n-by-n real symmetric matrix is the factorization ( in the complex Hermitian case), where Z is orthogonal (unitary) and is real and diagonal, with . The are the eigenvalues  of A, and the columns of Z are the eigenvectors . This is also often written . The eigendecomposition of a symmetric matrix is computed by the driver routines PxSYEV and PxSYEVX. The complex counterparts of these routines, which compute the eigendecomposition of complex Hermitian matrices, are the driver routines PxHEEV and PxHEEVX (see section 3.2.3).         

The approximate error bounds       for the computed eigenvalues are

The approximate error bounds for the computed eigenvectors , which bound the acute angles between the computed eigenvectors and true eigenvectors , are    

These bounds can be computed by the following code fragment:

      EPSMCH = PSLAMCH( ICTXT, 'E' )
*     Compute eigenvalues and eigenvectors of A
*     The eigenvalues are returned in W
*     The eigenvector matrix Z overwrites A
      CALL PSSYEV( 'V', UPLO, N, A, IA, JA, DESCA, W, Z, IZ, JZ,
     $             DESCZ, WORK, LWORK, INFO )
      IF( INFO.GT.0 ) THEN
         PRINT *,'PSSYEV did not converge'
      ELSE IF( N.GT.0 ) THEN
*        Compute the norm of A
         ANORM = MAX( ABS( W( 1 ) ), ABS( W( N ) ) )
         EERRBD = EPSMCH * ANORM
*        Compute reciprocal condition numbers for eigenvectors
         CALL SDISNA( 'Eigenvectors', N, N, W, RCONDZ, INFO )
         DO 10 I = 1, N
            ZERRBD( I ) = EPSMCH * ( ANORM / RCONDZ( I ) )
10       CONTINUE
      END IF

For example, if and



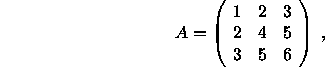
then the eigenvalues, approximate error bounds, and true errors are as follows.

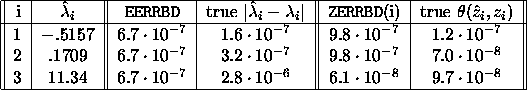
Further Details: Error Bounds for the Symmetric Eigenproblem 

The usual error analysis of the symmetric  eigenproblem using ScaLAPACK driver PSSYEV   (see subsection 3.2.3) is as follows [101]:

The computed eigendecomposition is nearly the exact eigendecomposition of A+E, namely, is a true eigendecomposition so that is orthogonal, where and . Here p(n) is a modestly growing function of n. We take p(n)=1 in the above code fragment. Each computed eigenvalue differs from a true by at most

Thus, large eigenvalues (those near ) are computed to high relative accuracy,   while small ones may not be.  

The angular difference between the computed unit eigenvector and a true unit eigenvector satisfies the approximate bound  

if is small enough. Here, is the absolute gap   between and the nearest other eigenvalue. Thus, if is close to other eigenvalues, its corresponding eigenvector may be inaccurate. The gaps may be easily computed from the array of computed eigenvalues by using subroutine SDISNA  . The gaps computed by SDISNA are ensured not to be so small as to cause overflow when used as divisors.    

Let be the invariant subspace spanned by a collection of eigenvectors , where is a subset of the integers from 1 to n. Let be the corresponding true subspace. Then

  where

is the absolute gap between the eigenvalues in and the nearest other eigenvalue. Thus, a cluster  of close eigenvalues that is far away from any other eigenvalue may have a well-determined invariant subspace even if its individual eigenvectors are ill-conditioned.

A small possibility exists that PSSYEV will fail to achieve the above error bounds on a heterogeneous network of processors   for reasons discussed in section 6.2. On a homogeneous network, PSSYEV is as robust as the corresponding LAPACK routine SSYEV. A future release will attempt to detect heterogeneity and warn the user to use an alternative algorithm.

In contrast to LAPACK, where the same error analysis applied to the simple and expert drivers, the expert driver PSSYEVX      satisfies slightly weaker error bounds than PSSYEV. The bounds and continue to hold, but the computed eigenvectors are no longer guaranteed to be orthogonal to one another. The corresponding LAPACK routine SSYEVX tries to guarantee orthogonality by reorthogonalizing computed eigenvectors against one another provided their corresponding computed eigenvalues are close enough together: , where the threshold . If m eigenvalues lie in a cluster satisfying this closeness criterion, the SSYEVX requires serial time to execute. When m is a large fraction of n, this serial bottleneck is expensive and does not always improve orthogonality.

ScaLAPACK addresses this problem in two ways. First, it lets the user use more or less time and space to perform reorthogonalization, rather than have a fixed criterion. In particular, the user can set the threshold ORTOL used above, decreasing it to make reorthogonalization less frequent or increasing it to reorthogonalize more. Furthermore, since each processor computes a subset of the eigenvectors, ScaLAPACK permits reorthogonalization only with the local eigenvectors; that is, no communication is allowed. Hence, if a cluster of eigenvalues is small enough for the corresponding eigenvectors to fit on one processor, the same reorthogonalization will be done as in LAPACK. The user can supply more or less workspace to limit the size of a cluster on one processor. Hence, at one extreme, with a large cluster and lots of workspace, the algorithm will be essentially equivalent to SSYEVX. At the other extreme, with all small clusters or little workspace supplied, the algorithm will be perfectly load balanced and perform minimal communication to compute the eigenvectors.

The second way ScaLAPACK will deal with reorthogonalization is to introduce a new algorithm [103, 102, 44] that requires nearly no reorthogonalization to compute orthogonal eigenvectors in a fully parallel way. This algorithm will be introduced in future ScaLAPACK and LAPACK releases.

In the special case of a real symmetric tridiagonal matrix T, the eigenvalues can sometimes be computed much more accurately. PxSYEV (and the other symmetric eigenproblem drivers) computes the eigenvalues and eigenvectors of a dense symmetric matrix by first reducing it to tridiagonal form  T and then finding the eigenvalues and eigenvectors of T. Reduction of a dense matrix to tridiagonal form  T can introduce additional errors, so the following bounds for the tridiagonal case do not apply to the dense case.

The eigenvalues of the symmetric tridiagonal matrix T may be computed with small componentwise relative backward error     () by using subroutine PxSTEBZ (section 3.3.4).    To compute tighter error bounds for the computed eigenvalues we must make some assumptions about T. The bounds discussed here are from [15]. Suppose T is positive definite, and write T=DHD where and . Then the computed eigenvalues can differ from true eigenvalues by

where p(n) is a modestly growing function of n. Thus, if is moderate, each eigenvalue will be computed to high relative accuracy,   no matter how tiny it is.