This section describes how one can estimate the execution time of a ScaLAPACK routine on a given platform, using Equation 5.1 and the values provided in table 5.5 and table 5.8. By comparing this estimate with experimental data, the user can determine whether reasonable performance has been achieved and can (possibly) identify the performance bottlenecks, if any.
For linear system
solvers, the estimate typically is
accurate to within 50%
for moderate-sized problems (i.e., 160,000 or more
matrix elements per node).
For eigensolvers,
the estimate may be low by a factor of 2
for moderate-sized problems and by more than that for smaller
problems. The eigensolvers take longer because they involve
matrix-vector flops, as well as matrix-matrix flops,
and involve
substantial numbers of o(
) flops that are not
included in the approximation.
The accuracy of performance estimates increases with the problem size.
Unfortunately,
because ScaLAPACK eigensolvers
require more memory than the other ScaLAPACK drivers,
large problems cannot be solved; hence, execution times
for small and medium-sized problems (rather than medium-sized
and large problems) are reported.
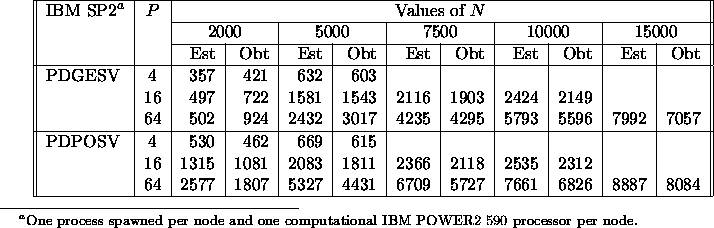
Table 5.16: Estimated (Est) versus obtained (Obt) Mflop/s rates of PDGESV
and PDPOSV on P nodes of the IBM SP2 computer for matrices of
order N and a block size (NB) equal to 50
Table 5.16 shows the estimated versus obtained Mflop/s rates for two ScaLAPACK driver routines solving linear systems of equations on the IBM Scalable POWERparallel 2 computer. The results show that for these drivers the estimated execution times are within approximately 35 % of the experimental data on the SP2. (The estimated times for the symmetric eigensolvers and SVD codes would not be as accurate.)