The final storage scheme we consider is for skyline matrices, which are also called variable band or profile matrices (see Duff, Erisman and Reid [80]). It is mostly of importance in direct solution methods, but it can be used for handling the diagonal blocks in block matrix factorization methods. A major advantage of solving linear systems having skyline coefficient matrices is that when pivoting is not necessary, the skyline structure is preserved during Gaussian elimination. If the matrix is symmetric, we only store its lower triangular part. A straightforward approach in storing the elements of a skyline matrix is to place all the rows (in order) into a floating-point array (val(:)), and then keep an integer array (row_ptr(:)) whose elements point to the beginning of each row. The column indices of the nonzeros stored in val(:) are easily derived and are not stored.
For a nonsymmetric skyline matrix such as the one illustrated in
Figure ![]() , we store the lower
triangular elements in SKS format, and store the upper triangular
elements in a column-oriented SKS format (transpose stored in row-wise
SKS format). These two separated substructures can be linked in
a variety of ways. One approach, discussed by Saad
in [186], is to store each row of the lower triangular
part and each column of the upper triangular part contiguously into
the floating-point array (val(:)). An additional pointer is
then needed to determine where the diagonal elements, which separate
the lower triangular elements from the upper triangular elements, are
located.
, we store the lower
triangular elements in SKS format, and store the upper triangular
elements in a column-oriented SKS format (transpose stored in row-wise
SKS format). These two separated substructures can be linked in
a variety of ways. One approach, discussed by Saad
in [186], is to store each row of the lower triangular
part and each column of the upper triangular part contiguously into
the floating-point array (val(:)). An additional pointer is
then needed to determine where the diagonal elements, which separate
the lower triangular elements from the upper triangular elements, are
located.
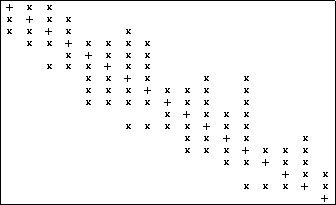
Figure: Profile of a nonsymmetric skyline or variable-band
matrix.