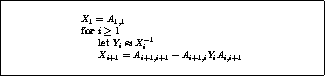
Figure: Incomplete block factorization of a block tridiagonal matrix
In many applications, a block tridiagonal structure can be found in the coefficient matrix. Examples are problems on a 2D regular grid if the blocks correspond to lines of grid points, and problems on a regular 3D grid, if the blocks correspond to planes of grid points. Even if such a block tridiagonal structure does not arise naturally, it can be imposed by renumbering the variables in a Cuthill-McKee ordering [60].
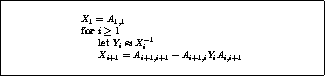
Figure: Incomplete block factorization of a block tridiagonal matrix
Such a matrix has incomplete block factorizations of a particularly
simple nature: since no fill can occur outside the diagonal
blocks  ,
all properties follow from our treatment of the pivot blocks. The
generating recurrence for the pivot blocks also takes a simple form,
see figure
,
all properties follow from our treatment of the pivot blocks. The
generating recurrence for the pivot blocks also takes a simple form,
see figure ![]() . After the factorization we are left
with sequences of
. After the factorization we are left
with sequences of 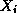 block forming the pivots, and of
block forming the pivots, and of 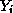 blocks
approximating their inverses.
blocks
approximating their inverses.