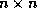 points. The variables
points. The variables
At first it may appear that the sequential time of solving a
factorization is of the order of the number of variables, but things
are not quite that bad. Consider the special case of central
differences on a regular domain of 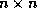 points. The variables
points. The variables

Figure: Wavefront solution of 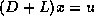 from a central difference problem
on a domain of
from a central difference problem
on a domain of 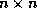 points.
points.
on any diagonal in the domain, that is,
in locations 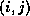 with
with 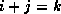 , depend
only on those on the previous diagonal, that is, with
, depend
only on those on the previous diagonal, that is, with 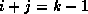 .
Therefore it is possible to process the operations on such a diagonal,
or `wavefront' ,
in parallel (see figure
.
Therefore it is possible to process the operations on such a diagonal,
or `wavefront' ,
in parallel (see figure ![]() ),
or have a vector computer pipeline them;
see Van der Vorst [205][203].
),
or have a vector computer pipeline them;
see Van der Vorst [205][203].
Another way of vectorizing the solution of the triangular factors is
to use some form of expansion of the inverses of the factors.
Consider for a moment a lower triangular matrix, normalized to
the form  where
where  is strictly lower triangular). Its
inverse can be given as either of the following two series:
is strictly lower triangular). Its
inverse can be given as either of the following two series:
(The first series is called a ``Neumann expansion'', the second an ``Euler expansion''. Both series are finite, but their length prohibits practical use of this fact.) Parallel or vectorizable preconditioners can be derived from an incomplete factorization by taking a small number of terms in either series. Experiments indicate that a small number of terms, while giving high execution rates, yields almost the full precision of the more recursive triangular solution (see Axelsson and Eijkhout [15] and Van der Vorst [201]).
There are some practical considerations in implementing these
expansion algorithms. For instance, because of the normalization the
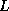 in equation (
in equation (![]() ) is not
) is not 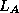 . Rather, if we
have a preconditioner (as described in section
. Rather, if we
have a preconditioner (as described in section ![]() )
described by
)
described by

then we write

Now we can choose whether or not to store the product 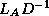 .
Doing so doubles the storage requirements for the matrix, not doing so
means that separate multiplications by
.
Doing so doubles the storage requirements for the matrix, not doing so
means that separate multiplications by 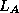 and
and 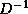 have to be
performed in the expansion.
have to be
performed in the expansion.
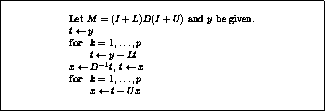
Figure: Preconditioning step algorithm for
a Neumann expansion 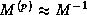 of an incomplete factorization
of an incomplete factorization 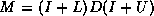 .
.
Suppose then that the products 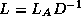 and
and 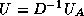 have been
stored. We then define
have been
stored. We then define 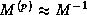 by
by
and replace solving a system 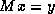 for
for  by computing
by computing 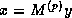 .
This algorithm is given in figure
.
This algorithm is given in figure ![]() .
.