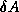 of the
coefficient matrix and
of the
coefficient matrix and 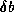 of the right hand side of a linear
system
of the right hand side of a linear
system 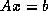 , such that the computed iterate
, such that the computed iterate 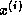 is the
solution of
is the
solution of 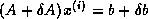 .
.
 for which there are nonnegative
constants
for which there are nonnegative
constants 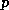 ,
, 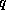 such that
such that 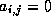 if
if 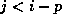 or
or 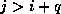 . The
two constants
. The
two constants 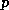 ,
, 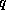 are called the left and right halfbandwidth
respectively.
are called the left and right halfbandwidth
respectively.
 as a
product of a lower triangular matrix
as a
product of a lower triangular matrix 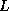 and its transpose
and its transpose 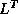 ,
that is,
,
that is, 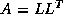 .
.
- Linear : some measure of the distance to the solution decreases by a constant factor in each iteration.
- Superlinear : the measure of the error decreases by a growing factor.
- Smooth : the measure of the error decreases in all or most iterations, though not necessarily by the same factor.
- Irregular : the measure of the error decreases in some iterations and increases in others. This observation unfortunately does not imply anything about the ultimate convergence of the method.
- Stalled : the measure of the error stays more or less constant during a number of iterations. As above, this does not imply anything about the ultimate convergence of the method.
 , the field of values is the
set
, the field of values is the
set 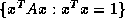 . For symmetric matrices this is the range
. For symmetric matrices this is the range
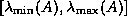 .
.
 but not
in an exact factorization of
but not
in an exact factorization of  . In an incomplete factorization,
some fill elements are discarded.
. In an incomplete factorization,
some fill elements are discarded.
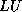 factorization of a
matrix
factorization of a
matrix  will in general satisfy
will in general satisfy 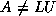 ; however, one hopes
that the factorization
; however, one hopes
that the factorization 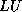 will be close enough to
will be close enough to  to function
as a preconditioner in an iterative method.
to function
as a preconditioner in an iterative method.
 and vector
and vector  , the
sequence of vectors
, the
sequence of vectors 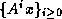 , or a finite initial part of
this sequence.
, or a finite initial part of
this sequence.
 for which
for which 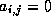 if
if 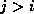 .
.
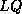 factorization
factorization
 as a product
of a lower triangular matrix
as a product
of a lower triangular matrix 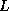 and a unitary matrix
and a unitary matrix 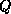 , that is,
, that is,
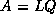 .
.
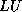 factorization /
factorization / 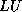 decomposition
decomposition
 as a product of a lower triangular matrix
as a product of a lower triangular matrix 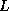 and an upper
triangular matrix
and an upper
triangular matrix 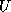 , that is,
, that is, 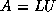 .
.
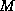 -Matrix
-Matrix

- Symmetric
- if
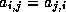 for all
for all  ,
, 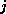 .
.
- Positive definite
- if it satisfies
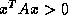 for all nonzero
vectors
for all nonzero
vectors  .
.
- Diagonally dominant
- if
 ; the
excess amount
; the
excess amount  is called
the diagonal dominance of the matrix.
is called
the diagonal dominance of the matrix.
- An
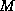 -matrix
-matrix
- if
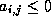 for
for 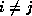 , and it is
nonsingular with
, and it is
nonsingular with  for all
for all  ,
, 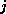 .
.
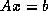 , either of the related
symmetric systems (
, either of the related
symmetric systems (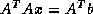 ) and (
) and (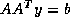 ;
;  ). For complex
). For complex  ,
, 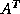 is replaced with
is replaced with 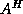 in the above
expressions.
in the above
expressions.
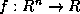 is called a vector norm
if
is called a vector norm
if
-
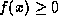 for all
for all  , and
, and 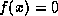 only if
only if 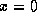 .
. -
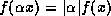 for all
for all  ,
,  .
.
-
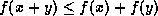 for all
for all  ,
, 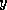 .
.
 ) are called a mutually
consistent pair if for all matrices
) are called a mutually
consistent pair if for all matrices  and vectors
and vectors 

- The natural ordering; this is the consecutive numbering by rows and columns.
- The red/black ordering; this is the numbering where all nodes
with coordinates
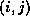 for which
for which 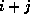 is odd are numbered
before those for which
is odd are numbered
before those for which 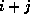 is even.
is even.
- The ordering by diagonals; this is the ordering where nodes
are grouped in levels for which
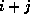 is constant. All nodes in
one level are numbered before the nodes in the next level.
is constant. All nodes in
one level are numbered before the nodes in the next level.
- The Cuthill-McKee ordering; this starts from one point, then numbers its neighbors, and continues numbering points that are neighbors of already numbered points. The Reverse Cuthill-McKee ordering then reverses the numbering; this may reduce the amount of fill in a factorization of the matrix.
- The Minimum Degree ordering; this orders the matrix rows by increasing numbers of nonzeros.
 in
a linear system
in
a linear system 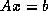 , then the residual corresponding to a
vector
, then the residual corresponding to a
vector 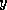 is
is 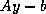 .
.
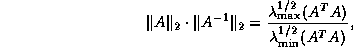
where  and
and 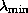 denote the largest and
smallest eigenvalues, respectively. For linear systems derived from
partial differential equations in 2D, the condition number is
proportional to the number of unknowns.
denote the largest and
smallest eigenvalues, respectively. For linear systems derived from
partial differential equations in 2D, the condition number is
proportional to the number of unknowns.
 is
is
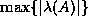 .
.
 for which
for which 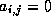 if
if 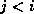 .
.