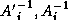 and
and 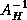 in
in
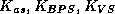 can be replaced by inexact solves
can be replaced by inexact solves
 and
and  ,
which can be standard elliptic preconditioners themselves
(e.g. multigrid, ILU, SSOR, etc.).
,
which can be standard elliptic preconditioners themselves
(e.g. multigrid, ILU, SSOR, etc.).
The exact solves involving 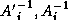 and
and 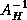 in
in
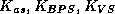 can be replaced by inexact solves
can be replaced by inexact solves
 and
and  ,
which can be standard elliptic preconditioners themselves
(e.g. multigrid, ILU, SSOR, etc.).
,
which can be standard elliptic preconditioners themselves
(e.g. multigrid, ILU, SSOR, etc.).
For the Schwarz methods, the modification is straightforward and the Inexact Solve Additive Schwarz Preconditioner is simply:
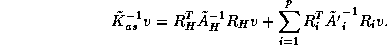
The Schur Complement methods require more changes to accommodate inexact solves. By replacing

by

in the definitions of

and

, we can easily obtain inexact preconditioners

and

for

. The main difficulty is, however, that the evaluation of the product

requires exact subdomain solves in

. One way to get around this is to use an inner iteration using

as a preconditioner for

in order to compute the action of

.
An alternative is to perform the iteration on the larger system
(![]() ) and construct a preconditioner from the
factorization in (
) and construct a preconditioner from the
factorization in (![]() ) by replacing the terms
) by replacing the terms

by

respectively, where

can be either

or

. Care must be taken to scale

and

so that they are as close to

and

as possible respectively - it is not sufficient that the condition number of

and

be close to unity, because the scaling of the coupling matrix

may be wrong.