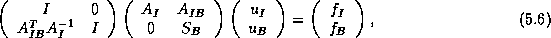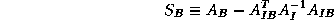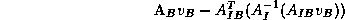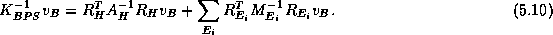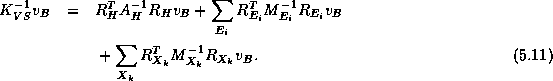Non-overlapping Subdomain Methods





Next: Further Remarks
Up: Domain Decomposition Methods
Previous: Overlapping Subdomain Methods
The easiest way to describe this approach is through
matrix notation.
The set of vertices of 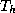 can be divided into two groups.
The set of interior vertices
can be divided into two groups.
The set of interior vertices 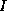 of
all
of
all 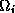 and the set of vertices
and the set of vertices 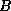 which lies on the boundaries
which lies on the boundaries
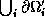 of the coarse triangles
of the coarse triangles 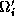 in
in 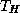 .
We shall re-order
.
We shall re-order  and
and 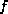 as
as 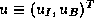 and
and 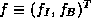 corresponding to this partition.
In this ordering, equation (
corresponding to this partition.
In this ordering, equation ( ) can be written
as follows:
) can be written
as follows:
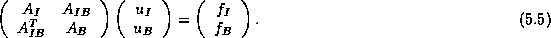
We note that since the subdomains are uncoupled by the boundary vertices,
 is block-diagonal
with each block
is block-diagonal
with each block 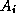 being the stiffness matrix corresponding
to the unknowns belonging to the interior
vertices of subdomain
being the stiffness matrix corresponding
to the unknowns belonging to the interior
vertices of subdomain 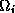 .
.
By a block LU-factorization of 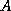 , the system in (
, the system in ( )
can be written as:
)
can be written as:
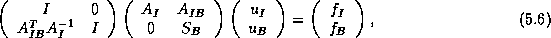
where
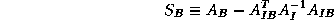
is the Schur complement of

in

.
By eliminating

in ( ), we arrive at
the following equation for
), we arrive at
the following equation for

:

We note the following properties of this Schur Complement system:
-

inherits the symmetric positive definiteness of

.
-

is dense in general and computing it explicitly
requires as many solves on each subdomain as there are
points on each of its edges.
- The condition number of

is

, an improvement
over the

growth for

.
- Given a vector

defined on the boundary vertices

of

,
the matrix-vector product

can be computed according to
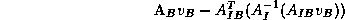
where

involves

independent subdomain solves using

.
- The right hand side

can also be computed using

independent subdomain solves.
These properties make it possible
to apply a preconditioned iterative method to ( ), which is
the basic method in the nonoverlapping substructuring approach.
We will also need some good preconditioners
to further improve the convergence of the Schur system.
), which is
the basic method in the nonoverlapping substructuring approach.
We will also need some good preconditioners
to further improve the convergence of the Schur system.
We shall first describe
the Bramble-Pasciak-Schatz preconditioner [36].
For this, we need to further decompose

into two non-overlapping
index sets:

where

denote the set of
nodes
corresponding to the vertices

's of

, and

denote the set of
nodes
on the edges

's
of the coarse triangles in

, excluding
the vertices
belonging to

.
In addition to the coarse grid interpolation and restriction
operators

defined before,
we shall also need a new set of interpolation and restriction
operators for the edges

's.
Let

be the pointwise restriction operator
(an

matrix, where

is the number
of vertices on the edge

)
onto the edge

defined by its action

if

but is zero otherwise.
The action of its transpose extends by zero a function
defined on

to one defined on

.
Corresponding to this partition of

,

can be written in
the block form:

The block

can again be block partitioned, with most of
the subblocks being zero. The diagonal blocks

of

are the
principal submatrices of

corresponding to

.
Each

represents the coupling of nodes on interface

separating two neighboring subdomains.
In defining the preconditioner, the action of

is
needed. However, as noted before, in general

is a dense
matrix which is also expensive to compute, and even if we had it, it
would be expensive to compute its action (we would need to compute its
inverse or a Cholesky factorization). Fortunately, many efficiently
invertible approximations to

have been proposed in the
literature (see Keyes and Gropp [136]) and we shall use these
so-called interface preconditioners for

instead.
We mention one specific preconditioner:

where

is an

one dimensional
Laplacian matrix, namely a tridiagonal matrix with

's down
the main diagonal and

's down the two off-diagonals,
and

is taken to be some average of the coefficient

of ( ) on the edge
) on the edge

.
We note that since the eigen-decomposition of

is known
and computable by the Fast Sine Transform, the action of

can be efficiently computed.
With these notations, the Bramble-Pasciak-Schatz preconditioner
is defined by its action on a vector

defined on

as follows:
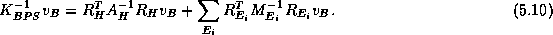
Analogous to the additive Schwarz preconditioner,
the computation of each term consists of the three steps
of restriction-inversion-interpolation and
is independent of the others and thus can be carried out in parallel.
Bramble, Pasciak and Schatz [36] prove that the condition
number of

is bounded by

. In
practice, there is a slight growth in the number of iterations as

becomes small (i.e., as the fine grid is refined) or as

becomes large (i.e., as the coarse grid becomes coarser).
The

growth is due to the coupling of the unknowns on the
edges incident on a common vertex

, which is not accounted for in

. Smith [191] proposed a vertex space
modification to

which explicitly accounts for this coupling
and therefore eliminates the dependence on

and

. The idea is
to introduce further subsets of

called vertex spaces

with

consisting of a small set of vertices on
the edges incident on the vertex

and adjacent to it. Note that

overlaps with

and

. Let

be the principal
submatrix of

corresponding to

, and

be
the corresponding restriction (pointwise) and extension (by zero)
matrices. As before,

is dense and expensive to compute and
factor/solve but efficiently invertible approximations (some using
variants of the

operator defined before) have been developed
in the literature (see Chan, Mathew and
Shao [52]). We shall let

be such a
preconditioner for

. Then Smith's Vertex Space
preconditioner is defined by:
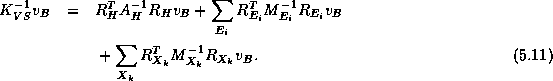
Smith [191] proved that the condition number
of

is bounded independent of

and

, provided
there is sufficient overlap of

with

.





Next: Further Remarks
Up: Domain Decomposition Methods
Previous: Overlapping Subdomain Methods
Jack Dongarra
Mon Nov 20 08:52:54 EST 1995
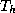 can be divided into two groups.
The set of interior vertices
can be divided into two groups.
The set of interior vertices 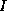 of
all
of
all 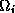 and the set of vertices
and the set of vertices 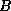 which lies on the boundaries
which lies on the boundaries
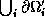 of the coarse triangles
of the coarse triangles 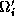 in
in 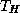 .
We shall re-order
.
We shall re-order  and
and 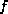 as
as 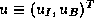 and
and 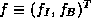 corresponding to this partition.
In this ordering, equation (
corresponding to this partition.
In this ordering, equation (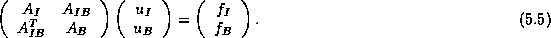
 is block-diagonal
with each block
is block-diagonal
with each block 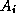 being the stiffness matrix corresponding
to the unknowns belonging to the interior
vertices of subdomain
being the stiffness matrix corresponding
to the unknowns belonging to the interior
vertices of subdomain 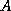 , the system in (
, the system in (