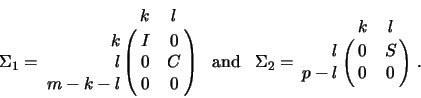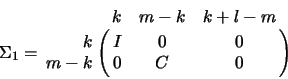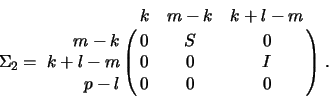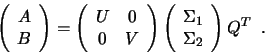Table 2.6:
Driver routines for generalized eigenvalue and singular value problems
| Type of |
Function and storage scheme |
Real/complex |
Complex |
| problem |
|
|
Hermitian |
| GSEP |
simple driver |
LA_SYGV (real only) |
LA_HEGV |
| |
divide and conquer driver |
LA_SYGVD (real only) |
LA_HEGVD |
| |
expert driver |
LA_SYGVX (real only) |
LA_HEGVX |
| |
simple driver (packed storage) |
LA_SPGV (real only) |
LA_HPGV |
| |
divide and conquer driver |
LA_SPGVD (real only) |
LA_HPGVD |
| |
expert driver |
LA_SPGVX (real only) |
LA_HPGVX |
| |
simple driver (band matrices) |
LA_SBGV (real only) |
LA_HBGV |
| |
divide and conquer driver |
LA_SBGVD (real only) |
LA_HBGVD |
| |
expert driver |
LA_SBGVX (real only) |
LA_HBGVX |
| GNEP |
simple driver for Schur factorization |
LA_GGES |
|
| |
expert driver for Schur factorization |
LA_GGESX |
|
| |
simple driver for eigenvalues/vectors |
LA_GGEV |
|
| |
expert driver for eigenvalues/vectors |
LA_GGEVX |
|
| GSVD |
singular values/vectors |
LA_GGSVD |
|
![]() matrix
matrix ![]() and a
and a
![]() matrix
matrix ![]() is given by the pair of factorizations
is given by the pair of factorizations
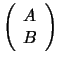 , and satisfies
, and satisfies