




Next: Computational Routines for the
Up: Computational Routines
Previous: Computational Routines for the
Contents
Index
Computational Routines for the Generalized Nonsymmetric Eigenproblem
LA_GGHRD
Real and complex versions.
SUBROUTINE LA_GGHRD( COMPQ, COMPZ, &
N, ILO, IHI, A, LDA, B, LDB, Q, LDQ, Z, &
LDZ, INFO )
CHARACTER(LEN=1), INTENT(IN) :: &
COMPQ, COMPZ
INTEGER, INTENT(IN) :: IHI, ILO, LDA, &
LDB, LDQ, LDZ, N
INTEGER, INTENT(OUT) :: INFO
type(wp), INTENT(INOUT) :: A(LDA,*), &
B(LDB,*), Q(LDQ,*), Z(LDZ,*)
where
type ::= REAL 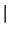 COMPLEX
COMPLEX
wp ::= KIND(1.0) 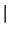 KIND(1.0D0)
KIND(1.0D0)
LA_GGHRD
reduces a pair of real / complex matrices 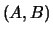 to generalized upper
Hessenberg form using orthogonal / unitary transformations.
to generalized upper
Hessenberg form using orthogonal / unitary transformations.
References: See [1] and [9,20].
-----------------------------------
LA_GGBAL
Real and complex versions.
SUBROUTINE LA_GGBAL( JOB, N, A, LDA, B, &
LDB, ILO, IHI, LSCALE, RSCALE, WORK, &
INFO )
CHARACTER(LEN=1), INTENT(IN) :: JOB
INTEGER, INTENT(IN) :: LDA, LDB, N
INTEGER, INTENT(OUT) :: IHI, ILO, INFO
REAL(wp), INTENT(OUT) :: LSCALE(*), &
RSCALE(*), WORK(*)
type(wp), INTENT(INOUT) :: A(LDA,*), B(LDB,*)
where
type ::= REAL 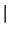 COMPLEX
COMPLEX
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_GGBAL balances a pair of general real / complex matrices 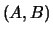 .
.
References: See [1] and [9,20,42].
-----------------------------------
LA_GGBAK
Real and complex versions.
SUBROUTINE LA_GGBAK( JOB, SIDE, N, ILO, &
IHI, LSCALE, RSCALE, M, V, LDV, INFO )
CHARACTER(LEN=1), INTENT(IN) :: JOB, &
SIDE
INTEGER, INTENT(IN) :: IHI, ILO, LDV, M, N
INTEGER, INTENT(OUT) :: INFO
REAL(wp), INTENT(IN) :: LSCALE(*), &
RSCALE(*)
type(wp), INTENT(INOUT) :: V(LDV,*)
where
type ::= REAL  COMPLEX
COMPLEX
wp ::= KIND(1.0)  KIND(1.0D0)
KIND(1.0D0)
LA_GGBAK
forms the right or left eigenvectors of a real / complex generalized
eigenvalue problem
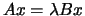 , by backward transformation on
the computed eigenvectors of the balanced pair of matrices output by
LA_GGBAL.
, by backward transformation on
the computed eigenvectors of the balanced pair of matrices output by
LA_GGBAL.
References: See [1] and [9,20,42].
-----------------------------------
LA_HGEQZ
Real version.
SUBROUTINE LA_HGEQZ( JOB, COMPQ, &
COMPZ, N, ILO, IHI, A, LDA, B, LDB, &
ALPHAR, ALPHAI, BETA, Q, LDQ, Z, LDZ, &
WORK, LWORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: COMPQ, &
COMPZ, JOB
INTEGER, INTENT(IN) :: IHI, ILO, LDA, LDB, &
LDQ, LDZ, LWORK, N
INTEGER, INTENT(OUT) :: INFO
REAL(wp), INTENT(INOUT) :: A(LDA,*), &
B(LDB,*), Q(LDQ,*), Z(LDZ,*)
REAL(wp), INTENT(OUT) :: ALPHAR(*), &
ALPHAI(*), BETA(*), WORK(LWORK)
where
wp ::= KIND(1.0) 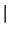 KIND(1.0D0)
KIND(1.0D0)
Complex version.
SUBROUTINE LA_HGEQZ( JOB, COMPQ, &
COMPZ, N, ILO, IHI, A, LDA, B, LDB, &
ALPHA, BETA, Q, LDQ, Z, LDZ, WORK, &
LWORK, RWORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: COMPQ, &
COMPZ, JOB
INTEGER, INTENT(IN) :: IHI, ILO, LDA, LDB, &
LDQ, LDZ, LWORK, N
INTEGER, INTENT(OUT) :: INFO
REAL(wp), INTENT(OUT) :: RWORK( * )
COMPLEX(wp), INTENT(INOUT) :: A(LDA,*), &
B(LDB,*), Q(LDQ,*), Z(LDZ,*)
COMPLEX(wp), INTENT(OUT) :: ALPHA(*), &
BETA(*), WORK(LWORK)
where
wp ::= KIND(1.0) 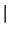 KIND(1.0D0)
KIND(1.0D0)
LA_HGEQZ
implements a single-shift version of the 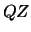 method for finding the generalized eigenvalues
method for finding the generalized eigenvalues
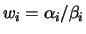 of the equation
of the equation
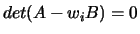
References: See [1] and [9,20,32].
-----------------------------------
LA_TGEVC
Real version.
SUBROUTINE LA_TGEVC( SIDE, HOWMNY, &
SELECT, N, A, LDA, B, LDB, VL, LDVL, &
VR, LDVR, MM, M, WORK, INFO )
CHARACTER(LEN=1), INTENT(IN) ::
HOWMNY, SIDE
INTEGER, INTENT(IN) :: LDA, LDB, LDVL,
LDVR, MM, N
INTEGER, INTENT(OUT) :: INFO, M
LOGICAL, INTENT(IN) :: SELECT(*)
REAL(wp), INTENT(IN) :: A(LDA,*), B(LDB,*)
REAL(wp), INTENT(INOUT) :: VL(LDVL,*), &
VR(LDVR,*)
REAL(wp), INTENT(OUT) :: WORK(*)
where
wp ::= KIND(1.0) 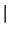 KIND(1.0D0)
KIND(1.0D0)
Complex version.
SUBROUTINE LA_TGEVC( SIDE, HOWMNY, &
SELECT, N, A, LDA, B, LDB, VL, LDVL, &
VR, LDVR, MM, M, WORK, RWORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: &
HOWMNY, SIDE
INTEGER, INTENT(IN) :: LDA, LDB, LDVL, &
LDVR, MM, N
INTEGER, INTENT(OUT) :: INFO, M
LOGICAL, INTENT(IN) :: SELECT(*)
REAL(wp), INTENT(OUT) :: RWORK(*)
COMPLEX(wp), INTENT(IN) :: A(LDA,*), &
B(LDB,*)
COMPLEX(wp), INTENT(INOUT) :: &
VL(LDVL,*), VR(LDVR,*)
COMPLEX(wp), INTENT(OUT) :: WORK(*)
where
wp ::= KIND(1.0) 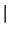 KIND(1.0D0)
KIND(1.0D0)
LA_TGEVC
computes some or all of the right and/or left generalized
eigenvectors of a pair of real / complex upper triangular matrices 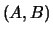 .
.
References: See [1] and [9,20].
-----------------------------------
LA_TGEXC
Real version.
SUBROUTINE LA_TGEXC( WANTQ, WANTZ, &
N, A, LDA, B, LDB, Q, LDQ, Z, LDZ, IFST, &
ILST, WORK, LWORK, INFO )
LOGICAL, INTENT(IN) :: WANTQ, WANTZ
INTEGER, INTENT(IN) :: LDA, LDB, LDQ, &
LDZ, LWORK, N
INTEGER, INTENT(INOUT) :: IFST, ILST
INTEGER, INTENT(OUT) :: INFO
REAL(wp), INTENT(INOUT) :: A(LDA,*), &
B(LDB,*), Q(LDQ,*), Z(LDZ,*)
REAL(wp), INTENT(OUT) :: WORK(LWORK)
where
wp ::= KIND(1.0) 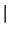 KIND(1.0D0)
KIND(1.0D0)
Complex version.
SUBROUTINE LA_TGEXC( WANTQ, WANTZ, &
N, A, LDA, B, LDB, Q, LDQ, Z, LDZ, IFST, &
ILST, INFO )
LOGICAL, INTENT(IN) :: WANTQ, WANTZ
INTEGER, INTENT(IN) :: LDA, LDB, LDQ, &
LDZ, N
INTEGER, INTENT(INOUT) :: IFST, ILST
INTEGER, INTENT(OUT) :: INFO
COMPLEX(wp), INTENT(INOUT) :: A(LDA,*), &
B(LDB,*), Q(LDQ,*), Z(LDZ,*)
where
wp ::= KIND(1.0) 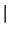 KIND(1.0D0)
KIND(1.0D0)
LA_TGEXC
reorders the generalized Schur decomposition of a complex
matrix pair 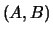 , using an orthogonal / unitary equivalence transformation
, using an orthogonal / unitary equivalence transformation
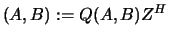 , so that the diagonal block of
, so that the diagonal block of 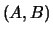 with
row index IFST is moved to row ILST.
with
row index IFST is moved to row ILST.
References: See [1] and [9,20,28].
-----------------------------------
LA_TGSYL
Real and complex versions.
SUBROUTINE LA_TGSYL( TRANS, IJOB, M, N, &
A, LDA, B, LDB, C, LDC, D, LDD, E, LDE, &
F, LDF, SCALE, DIF, WORK, LWORK, &
IWORK, INFO )
CHARACTER, INTENT(IN) :: TRANS
INTEGER, INTENT(IN) :: IJOB, LDA, LDB, &
LDC, LDD, LDE, LDF, LWORK, M, N
INTEGER, INTENT(OUT) :: INFO, IWORK(*)
REAL(wp), INTENT(OUT) :: DIF, SCALE
type(wp), INTENT(IN) :: A(LDA,*), B(LDB,*), &
D(LDD,*), E(LDF,*)
type(wp), INTENT(INOUT) :: C(LDC,*), &
F(LDF,*)
type(wp), INTENT(OUT) :: WORK(LWORK)
where
type ::= REAL 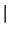 COMPLEX
COMPLEX
wp ::= KIND(1.0) 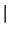 KIND(1.0D0)
KIND(1.0D0)
LA_TGSYL
solves the generalized Sylvester equation.
References: See [1] and [9,20,26,24,27].
-----------------------------------
LA_TGSNA
Real and complex versions.
SUBROUTINE LA_TGSNA( JOB, HOWMNY, &
SELECT, N, A, LDA, B, LDB, VL, LDVL, &
VR, LDVR, S, DIF, MM, M, WORK, &
LWORK, IWORK, INFO )
CHARACTER(LEN=1), INTENT(IN) :: &
HOWMNY, JOB
INTEGER, INTENT(IN) :: LDA, LDB, LDVL, &
LDVR, LWORK, MM, N
INTEGER, INTENT(OUT) :: INFO, M, IWORK(*)
LOGICAL, INTENT(IN) :: SELECT(*)
REAL(wp), INTENT(OUT) :: DIF(*), S(*)
type(wp), INTENT(IN) :: A(LDA,*), &
B(LDB,*), VL(LDVL,*), VR(LDVR,*)
type(wp), INTENT(OUT) :: WORK(LWORK)
where
type ::= REAL 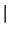 COMPLEX
COMPLEX
wp ::= KIND(1.0) 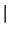 KIND(1.0D0)
KIND(1.0D0)
LA_TGSNA
estimates reciprocal condition numbers for specified
eigenvalues and/or eigenvectors of a matrix pair 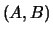 .
.
References: See [1] and
[9,20,25,28,26].
-----------------------------------
LA_TGSEN
Real version.
SUBROUTINE LA_TGSEN( IJOB, WANTQ, &
WANTZ, SELECT, N, A, LDA, B, LDB, &
ALPHAR, ALPHAI, BETA, Q, LDQ, Z, LDZ, &
M, PL, PR, DIF, WORK, LWORK, IWORK, &
LIWORK, INFO )
LOGICAL, INTENT(IN) :: WANTQ, WANTZ
INTEGER, INTENT(IN) :: IJOB, LDA, LDB, &
LDQ, LDZ, LIWORK, LWORK, N
INTEGER, INTENT(OUT) :: INFO, M,&
IWORK(LIWORK)
REAL(wp), INTENT(OUT) :: PL, PR
LOGICAL, INTENT(IN) :: SELECT(*)
REAL(wp), INTENT(INOUT) :: A(LDA,*), &
B(LDB,*), Q(LDQ,*), Z(LDZ,*)
REAL(wp), INTENT(OUT) :: ALPHAI(*), &
ALPHAR(*), BETA(*), DIF(2), &
WORK(LWORK)
where
wp ::= KIND(1.0) 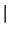 KIND(1.0D0)
KIND(1.0D0)
Complex version.
SUBROUTINE LA_TGSEN( IJOB, WANTQ, &
WANTZ, SELECT, N, A, LDA, B, LDB, &
ALPHA, BETA, Q, LDQ, Z, LDZ, &
M, PL, PR, DIF, WORK, LWORK, IWORK, &
LIWORK, INFO )
LOGICAL, INTENT(IN) :: WANTQ, WANTZ
INTEGER, INTENT(IN) :: IJOB, LDA, LDB, &
LDQ, LDZ, LIWORK, LWORK, N
INTEGER, INTENT(OUT) :: INFO, M, &
IWORK(LIWORK)
REAL(wp), INTENT(OUT) :: PL, PR
LOGICAL, INTENT(IN) :: SELECT(*)
REAL(wp), INTENT(OUT) :: DIF(2)
COMPLEX(wp), INTENT(INOUT) :: A(LDA,*), &
B(LDB,*), Q(LDQ,*), Z(LDZ,*)
COMPLEX(wp), INTENT(OUT) :: ALPHA(*), &
BETA(*), WORK(LWORK)
where
wp ::= KIND(1.0) 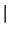 KIND(1.0D0)
KIND(1.0D0)
LA_TGSEN
reorders the generalized Schur decomposition of a real / complex
matrix pair 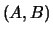 (in terms of an orthogonal / unitary equivalence
transformation
(in terms of an orthogonal / unitary equivalence
transformation 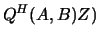 , so that a selected cluster of eigenvalues
appears in the leading diagonal blocks of the pair
, so that a selected cluster of eigenvalues
appears in the leading diagonal blocks of the pair 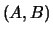 .
.
References: See [1] and
[9,20,28,25,26].
-----------------------------------





Next: Computational Routines for the
Up: Computational Routines
Previous: Computational Routines for the
Contents
Index
Susan Blackford
2001-08-19